Cho hình chóp S.ABC có tam giác ABC đều cạnh \(a = 3cm,\,\,SA \bot \left( {ABC} \right)\) và \(SA = 2a\). Tính thể tích khối cầu ngoại tiếp hình chóp \(S.ABC\)

D. \(16\pi \sqrt 3 \,c{m^3}\)

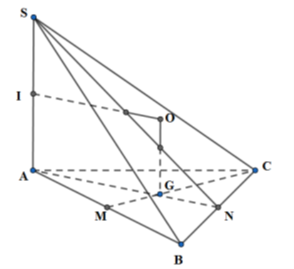
Gọi M, N, I lần lượt là trung điểm của AB, BC, SA; G là trọng tâm tâm giác ABC

Mà tam giác ABC đều \( \Rightarrow \) G là tâm đường tròn ngoại tiếp tam giác ABC

Trong (SAN), dựng đường thẳng qua G song song SA, đường thẳng qua I song song AN, chúng cắt nhau tại O

Khi đó, \(OA = OB = OC = OS\) hay O là tâm mặt cầu ngoại tiếp hình chóp S.ABC

I là trung điểm của SA \( \Rightarrow IA = \frac{{SA}}{2} = \frac{{2a}}{2} = a = 3\left( {cm} \right)\)

Tam giác đều cạnh ABC \(a = 3cm \Rightarrow AN = \frac{{a\sqrt 3 }}{2} \Rightarrow AG = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3} = \frac{{3.\sqrt 3 }}{3} = \sqrt 3 \left( {cm} \right)\)

Tứ giác AGOI có: \(OG//AI,\,\,\,OI//AG \Rightarrow \) AGOI là hình bình hành

Mà \(A = {90^0} \Rightarrow \) AGOI là hình chữ nhật \( \Rightarrow OA = \sqrt {A{I^2} + A{G^2}} = \sqrt {{3^2} + {{\left( {\sqrt 3 } \right)}^2}} = 2\sqrt 3 \left( {cm} \right)\)

\( \Rightarrow \) Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là: \(R = 2\sqrt 3 \left( {cm} \right)\)

\( \Rightarrow \) Thể tích khối cầu ngoại tiếp hình chóp S.ABC là: \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi .{\left( {2\sqrt 3 } \right)^3} = 32\sqrt 3 \pi \left( {c{m^3}} \right)\)