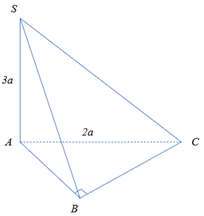
Cho hình chóp S.ABC có SA = 3a và SA vuông góc với đáy, tam giác ABC là tam giác vuông cân tại B, AC = 2a. Tính thể tích V của khối chóp S.ABC. A. V = a^3/3 B. V = 2a^3/3 C. V = 2a^3
Cho hình chóp \(S.ABC\) có \(SA = 3a\) và \(SA\) vuông góc với đáy, tam giác \(ABC\) là tam giác vuông cân tại \(B\), \(AC = 2a\). Tính thể tích \(V\) của khối chóp \(S.ABC\).
A. \(V = \frac{{{a^3}}}{3}\).
B. \(V = \frac{{2{a^3}}}{3}\).
C. \(V = 2{a^3}\).
D. \(V = {a^3}\).