Cho hình chóp S.ABC có đáy là tam giác vuông tại B. Biết Delta SAB là tam giác đều và thuộc mặt phẳng vuông góc với mặt phẳng ( ABC ). Biết AB = a, AC = a căn bậc hai của 3. Thể tích khối chó
64
25/04/2024
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(B\). Biết \(\Delta SAB\) là tam giác đều và thuộc mặt phẳng vuông góc với mặt phẳng \(\left( {ABC} \right)\). Biết \(AB = a\), \(AC = a\sqrt 3 \). Thể tích khối chóp \(S.ABC\) là:
A. \(\frac{{{a^3}}}{4}\).
B. \(\frac{{{a^3}\sqrt 6 }}{4}\).
C. \(\frac{{{a^3}\sqrt 2 }}{6}\).
D. \(\frac{{{a^3}\sqrt 6 }}{{12}}\).
Trả lời
Lời giải
Chọn D
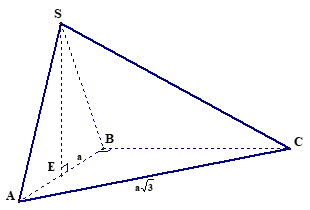
Gọi \(E\) là trung điểm cạnh \(AB\). Ta có:
\(\left. \begin{array}{l}\left( {SAB} \right) \bot \left( {ABC} \right)\\\left( {SAB} \right) \cap \left( {ABC} \right) = AB\\Trong{\rm{ }}\left( {SAB} \right):SE \bot AB\end{array} \right\} \Rightarrow SE \bot \left( {ABC} \right)\) tại \(E\).
Mà \(\Delta SAB\) là tam giá đều có cạnh \(AB = a\) \( \Rightarrow SE = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\).
\(\Delta ABC\) vuông tại \(B\) \( \Rightarrow BC = \sqrt {A{C^2} - A{B^2}} = a\sqrt 2 \) \( \Rightarrow {S_{\Delta ABC}} = \frac{1}{2}AB.BC = \frac{{{a^2}\sqrt 2 }}{2}\).
Vậy \({V_{S,ABC}} = \frac{1}{3}SE.{S_{\Delta ABC}} = \frac{1}{3}\frac{{a\sqrt 3 }}{2}.\frac{{{a^2}\sqrt 2 }}{2} = \frac{{{a^3}\sqrt 6 }}{{12}}\).

