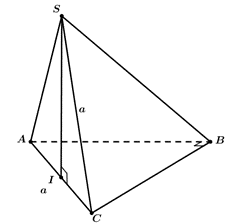
Cho hình chóp (S.ABC) có đáy là tam giác vuông cân tại (B). Hình chiếu của (S) trên mặt phẳng ( ABC) trùng với trung điểm I của cạnh AC, biết rằng tam giác SAC đều cạnh a. Tính thể tích V của
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông cân tại \(B\). Hình chiếu của \(S\) trên mặt phẳng \(\left( {ABC} \right)\) trùng với trung điểm \(I\) của cạnh \(AC\), biết rằng tam giác \(SAC\) đều cạnh \(a\). Tính thể tích \(V\) của khối chóp \(S.ABC\).
A. \(V = \frac{{{a^3}}}{{24}}\).
B. \(V = \frac{{\sqrt 3 {a^3}}}{{48}}\).
C. \(V = \frac{{\sqrt 3 {a^3}}}{6}\).
D. \(V = \frac{{\sqrt 3 {a^3}}}{{24}}\).