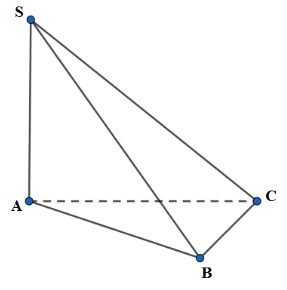
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A . Biết SA vuông góc với đáy ABC và \[AB = a,\,\,AC = 2a,\,\,\,SC = 3a\] . Thể tích khối chóp S.ABC là:

D. \(\frac{{{a^3}}}{4}\)

Đáp án B

Phương pháp:

Thể tích khối chóp: \(V = \frac{1}{3}Sh\)

Cách giải:

ABC là tam giác vuông tại A \( \Rightarrow {S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.a.2a = {a^2}\)

SAC là tam giác vuông tại A

\( \Rightarrow SA = \sqrt {S{C^2} - A{C^2}} = \sqrt {{{\left( {3a} \right)}^2} - {{\left( {2a} \right)}^2}} = a\sqrt 5 \)

Thể tích khối chóp S.ABC là: \(V = \frac{1}{3}{S_{ABC}}.SA = \frac{1}{3}{a^2}.a\sqrt 5 = \frac{{{a^3}\sqrt 5 }}{3}\)