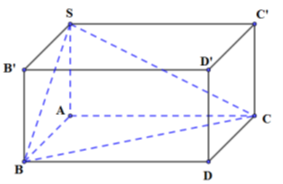
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, biết SA vuông góc (ABC), SA = a, AB = 2a, AC = 3a
36
30/04/2024
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, biết \(SA \bot \left( {ABC} \right),\,\,SA = a,\,\,AB = 2a,\,\,AC = 3a\). Tính bán kính r của mặt cầu ngoại tiếp hình chóp S.ABC.
A. \(r = \frac{{\sqrt {13} }}{{13}}a\)
B. \(r = \frac{3}{2}a\)
C. \(r = a\sqrt {14} \)
D. \(r = \frac{{\sqrt {14} }}{2}a\)
Trả lời
Đáp án D
Phương pháp:
S.ABC là tứ diện vuông là một phần của hình hộp chữ nhật SB’D’C’.ABCD (như hình vẽ bên), có tâm mặt cầu ngoại tiếp trùng với tâm của hình hộp chữ nhật, có bán kính bằng nửa đường chéo của hình hộp chữ nhật (độ dài các cạnh là a, b, c) bằng \(r = \frac{{\sqrt {{a^2} + {b^2} + {c^2}} }}{2}\)
Cách giải:
Bán kính r của mặt cầu ngoại tiếp hình chóp S.ABC : \(r = \frac{{\sqrt {S{A^2} + B{A^2} + C{A^2}} }}{2} = \frac{{\sqrt {{a^2} + {{\left( {2a} \right)}^2} + {{\left( {3a} \right)}^2}} }}{2} = \frac{{a\sqrt {14} }}{2}\)
