Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, ABC = 30 độ. Tam giác ABC là tam giác
42
28/04/2024
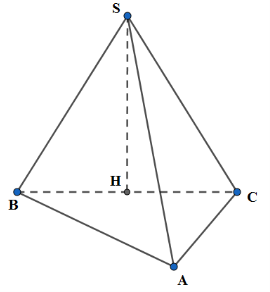
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, \(ABC = {30^0}\). Tam giác SBC là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp S.ABC là:
A. \(\frac{{{a^3}}}{{16}}\)
B. \(\frac{{3\sqrt 3 {a^3}}}{{16}}\)
C. \(\frac{{3{a^3}}}{{16}}\)
D. \(\frac{{\sqrt 3 {a^3}}}{{16}}\)
Trả lời
Đáp án A
Cách giải:
Kẻ \(SH \bot BC,\,\,H \in BC\)
Do \(\left( {SBC} \right) \bot \left( {ABC} \right),\,\,\,\left( {SBC} \right) \cap \left( {ABC} \right) = BC \Rightarrow SH \bot \left( {ABC} \right)\)
\(\Delta SBC\) đều, cạnh a\( \Rightarrow SH = \frac{{a\sqrt 3 }}{2}\)
\(\Delta ABC\) vuông tại A có \(ABC = {30^0} \Rightarrow ABC\) là một nửa tam giác đều cạnh là \(BA = a \Rightarrow {S_{ABC}} = \frac{1}{2}.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{8}\)
Thể tích khối chóp S.ABC là:
\(V = \frac{1}{3}SH.{S_{ABC}} = \frac{1}{3}.\frac{{a\sqrt 3 }}{2}.\frac{{{a^2}\sqrt 3 }}{8} = \frac{{{a^3}}}{{16}}\)