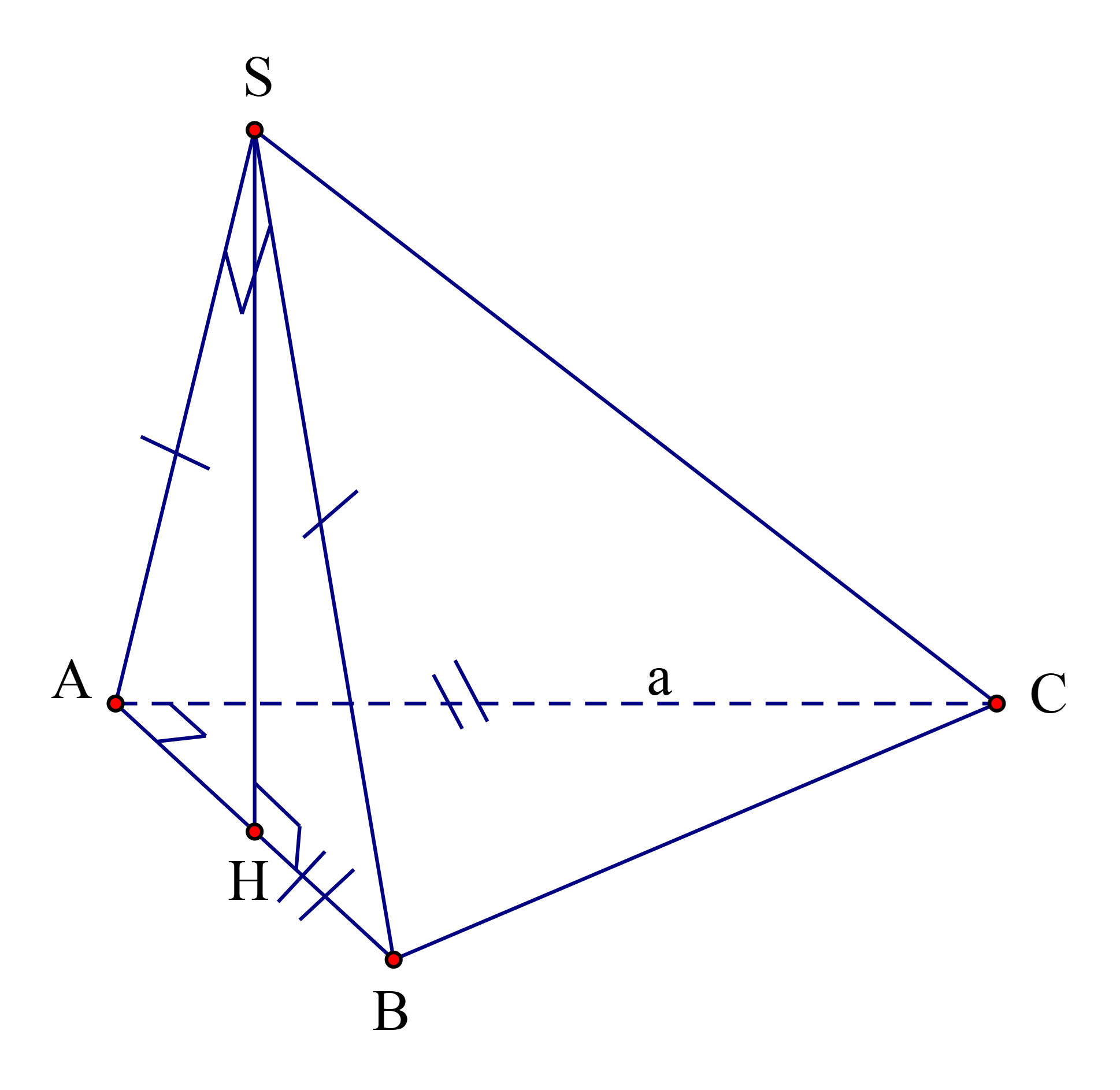
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân; AB = AC = a; mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC
Cho hình chóp \(S.ABC\)có đáy \(ABC\)là tam giác vuông cân; \(AB = AC = a\); mặt bên \(SAB\)là tam giác vuông cân tại \(S\)và nằm trong mặt phẳng vuông góc với đáy. Tính theo \(a\)thể tích của khối chóp \(S.ABC\).
A. \[\frac{1}{{12}}{a^3}\].
B. \[\frac{{\sqrt 3 }}{4}{a^3}\].
C. \[\frac{{\sqrt 3 }}{{12}}{a^3}\].
D. \[\frac{1}{4}{a^3}\].