Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa mặt bên với đáy bằng 45 độ C. Gọi M, N, P
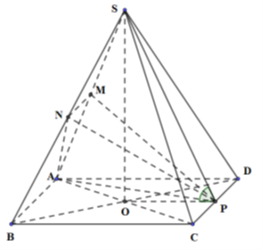
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa mặt bên với đáy bằng \({45^0}\). Gọi M, N, P lần lượt là trung điểm của SA, SB, SC. Tính thể tích của khối tứ diện AMNP.
D. \(\frac{{{a^3}}}{{24}}\)