Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng a căn bậc hai của 21/6. Tính theo a thể tích V của khối chóp S.ABC A. V = a^3 căn bậc hai của 3/12 B. V = a^3 căn bậc hai của
34
27/04/2024
Cho hình chóp đều \[S.ABC\] có cạnh đáy bằng \[a\], cạnh bên bằng \[\frac{{a\sqrt {21} }}{6}\]. Tính theo \(a\) thể tích \(V\) của khối chóp \[S.ABC\].
A. \[V = \frac{{{a^3}\sqrt 3 }}{{12}}\].
B. \[V = \frac{{{a^3}\sqrt 3 }}{8}\].
C. \[V = \frac{{{a^3}\sqrt 3 }}{6}\].
D. \[V = \frac{{{a^3}\sqrt 3 }}{{24}}\].
Trả lời
Lời giải
Chọn D
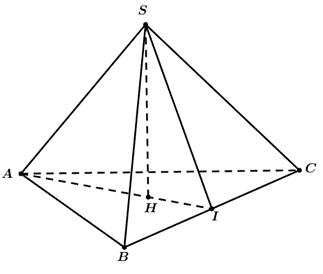
Gọi \[I\] là trung điểm của cạnh \[BC\], \[H\] là trọng tâm của tam giác \[ABC\] ta có: \[SH \bot \left( {ABC} \right)\] và\[SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {S{A^2} - {{\left( {\frac{2}{3}AI} \right)}^2}} = \sqrt {{{\left( {\frac{{a\sqrt {21} }}{6}} \right)}^2} - {{\left( {\frac{2}{3}.\frac{{a\sqrt 3 }}{2}} \right)}^2}} = \frac{a}{2}.\]
Vậy \[V = \frac{1}{3}.SH.{S_{\Delta ABC}} = \frac{1}{3}.\frac{a}{2}.\frac{1}{2}a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{{24}}.\]

