Cho hình chóp đều S.ABC có AB = 2 căn bậc hai của 3, mặt bên tạo với đáy một góc 45^0 Thể tích của khối chóp S.ABC bằng A. 2 căn bậc hai của 3 B. 4 căn bậc hai của 3 C. 8 căn bậc hai
40
26/04/2024
Cho hình chóp đều \[S.ABC\] có \[AB = 2\sqrt 3 \], mặt bên tạo với đáy một góc \[{45^0}\].
Thể tích của khối chóp \[S.ABC\] bằng
A. \[2\sqrt 3 \].
B. \[4\sqrt 3 \].
C. \[8\sqrt 3 \].
D. \[\sqrt 3 \].
Trả lời
Lời giải
Gọi \[D\] là trung điểm của \[BC\] và \[E\] là trọng tâm \[\Delta ABC\]. Do \[S.ABC\] là hình chóp đều nên \[SE\] là đường cao của hình chóp. Ta có:
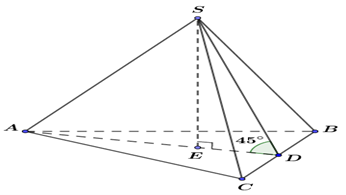
\[\left\{ {\begin{array}{*{20}{c}}{\left( {SBC} \right) \cap \left( {ABC} \right) = BC}\\{SD \bot BC,\,\,SD \subset \left( {SBC} \right)}\\{AD \bot BC,\,\,AD \subset \left( {ABC} \right)}\end{array}} \right.\]
Góc giữa hai mặt phẳng \[\left( {SBC} \right)\] và \[\left( {ABC} \right)\] là góc giữa \[SD\] và \[AD\], đó là \[\widehat {SDA}\]. Theo bài ra \[\widehat {SDA} = {45^0}\].
\[{\mathcal{B}_{ABC}} = {\left( {2\sqrt 3 } \right)^2}\frac{{\sqrt 3 }}{4} = 3\sqrt 3 \].
\[AD = 2\sqrt 3 .\frac{{\sqrt 3 }}{2} = 3\]; \[ED = \frac{1}{3}AD = \frac{1}{3}.3 = 1\].
Tam giác \[SED\] vuông tại \[E\] có \[\widehat {SDE} = {45^0}\] nên tam giác \[SED\] vuông cân tại \[E\].
Do đó \[SE = ED = 1\].
\[{V_{S.ABC}} = \frac{1}{3}{\mathcal{B}_{ABC}}.SE = \frac{1}{3}.3\sqrt 3 .1 = \sqrt 3 \].

