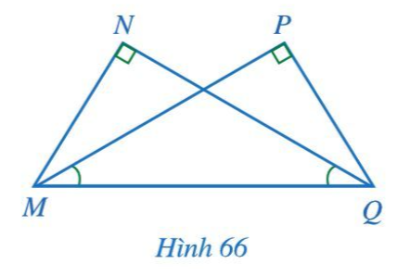
Cho Hình 66 có góc N = góc P = 90°, góc PMQ = góc NQM. Chứng minh MN = QP, MP = QN
Bài 3 trang 92 Toán 7 Tập 2:
Cho Hình 66 có ˆN=ˆP=90° Chứng minh MN = QP, MP = QN.
Bài 3 trang 92 Toán 7 Tập 2:
Cho Hình 66 có ˆN=ˆP=90° Chứng minh MN = QP, MP = QN.

|
GT |
MNQ, MPQ,
|
|
KL |
MN = QP, MP = QN. |
Chứng minh (Hình 66):
Tam giác MNQ có (giả thiết) nên tam giác MNQ vuông tại N.
Tam giác QPM có (giả thiết) nên tam giác MPQ vuông tại P.
Xét MNQ (vuông tại N) và MPQ (vuông tại P) có:
(giả thiết).
MQ chung.
Suy ra MNQ = QPM (cạnh huyền - góc nhọn).
Do đó MN = QP và MP = QN (các cặp cạnh tương ứng).
Vậy MN = QP và MP = QN.
Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh
Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh
Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc