Có ba trạm quan sát A, B, C trong đó trạm quan sát C ở giữa hồ
221
16/11/2023
Câu hỏi khởi động trang 88 Toán 7 Tập 2: Có ba trạm quan sát A, B, C trong đó trạm quan sát C ở giữa hồ.
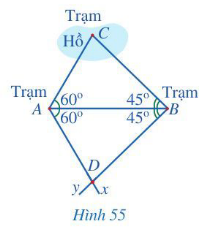
Người ta muốn đo khoảng cách từ A và từ B đến C. Do không thể đo trực tiếp được các khoảng cách trên nên người ta làm như sau (Hình 55):
- Đo góc BAC được 60°, đo góc ABC được 45°;
- Kẻ tia Ax sao cho ^BAx=60°, kẻ tia By sao cho , xác định giao điểm D của hai tia đó;
- Đo khoảng cách AD và BD. Ta có AC = AD và BC = BD.
Tại sao lại có hai đẳng thức trên?
Trả lời
Bài toán được mô tả bởi hai tam giác ABC và tam giác ABD như Hình 55.
|
GT
|
ABC, ABD,
|
|
KL
|
AC = AD và BC = BD.
|
Chứng minh (Hình 55):
Xét ABC và ABD có:
(giả thiết),
AB chung,
(giả thiết)
Suy ra ABC = ABD (g.c.g)
Do đó AC = AD và BC = BD (các cặp cạnh tương ứng).
Vậy AC = AD và BC = BD.
Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh
Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh
Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc
Bài 7: Tam giác cân
Bài 8: Đường vuông góc và đường xiên
Bài 9: Đường trung trực của một đoạn thẳng

