Cho hàm y = f(x) liên tục trên đoạn [ - 2; 2] và có đồ thị như hình vẽ bên. Số nghiệm của phương trình 3f(x + 2) - 4 = 0 trên đoạn [ - 2; 2] là ? A. 4 B. 2 C. 3 D. 1
72
27/04/2024
Cho hàm y=f(x) liên tục trên đoạn [−2;2] và có đồ thị như hình vẽ bên.
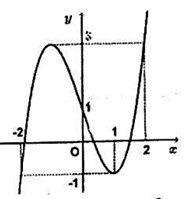
Số nghiệm của phương trình 3f(x+2)−4=0 trên đoạn [−2;2] là ?
A. 4.
B. 2.
C. 3.
D. 1.
Trả lời
Lời giải
Chọn D
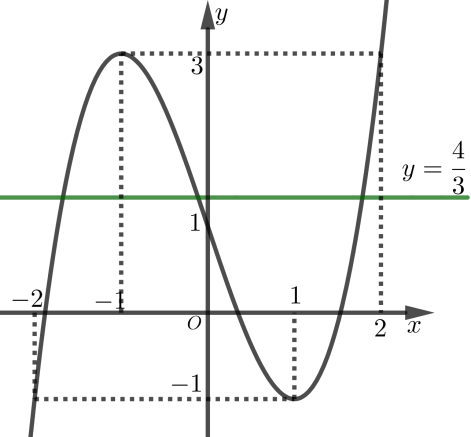
Xét phương trình 3f(x+2)−4=0⇔f(x+2)=43 (1)
Đặt X=x+2, do −2≤x≤2⇔0≤x+2≤4⇔0≤X≤4 . Khi đó ta có (1)⇔f(X)=43(∗)
Vậy phương trình (1)có nghiệm trên đoạn [−2;2] khi và chỉ khi phương trình (∗) có nghiệm trên đoạn [0;4].
Dựa vào hình vẽ ta nhận thấy trên đoạn [0;4] thì đường thẳng y=43 cắt đồ thị hàm số đã cho tại đúng một điểm. Do đó phương trình (∗) có đúng 1 nghiệm hay phương trình (1) có đúng một nghiệm.


