Cho hàm số f(x). Tìm các giới hạn sau: lim(x->1+) f(x); lim(x->1-) f(x); lim (x->1) f(x) (nếu có)
Bài 2 trang 79 Toán 11 Tập 1: Cho hàm số 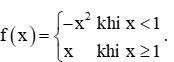
Tìm các giới hạn sau: limx→1+f(x);limx→1−f(x);limx→1f(x) (nếu có).
Bài 2 trang 79 Toán 11 Tập 1: Cho hàm số 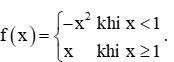
Tìm các giới hạn sau: limx→1+f(x);limx→1−f(x);limx→1f(x) (nếu có).
+) Với dãy số (xn) bất kì, xn ≤ 1 và xn → 1. Khi đó f(xn) = −x2n nên limf(xn) = lim(−x2n)=−1.
Vì vậy limx→1−f(x)=−1.
+) Với dãy số (xn) bất kì, xn > 1 và xn → 1. Khi đó f(xn) = xn nên limf(xn) = lim(xn) = 1.
Vì vậy limx→1+f(x)=1.
+) Vì limx→1+f(x)≠limx→1−f(x) nên không tồn tại limx→1f(x).
Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác: