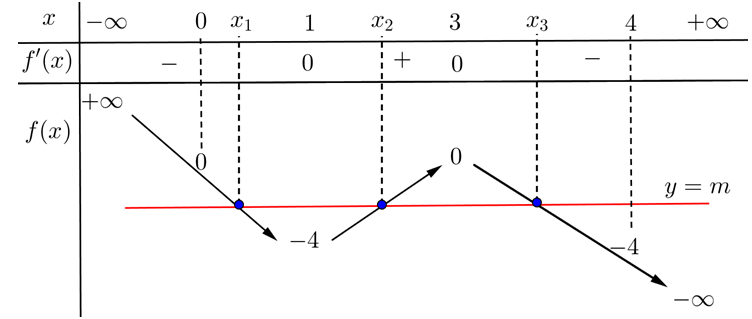
Cho hàm số $y=x^3-6x^2+9x+m\left(C\right)$, với m là tham số. Giả sử đồ thị (C) cắt trục hoành tại ba điểm phân biệt có hoành độ thỏa mãn $x_1<x_2<x_3$. Khẳng định nào sau đây đúng?

Chọn C

Phương trình hoành độ giao điểm của đồ thị (C) với trục hoành $x^3-6x^2+9x+m=0\iff m=-x^3+6x^2-9x$ (1). Xét hàm số $f\left(x\right)=-x^3+6x^2-9x$ với $x\in ℝ$

Ta có $f\text{'}\left(x\right)=-3x^2+12x-9=0\iff \left[\begin{array}{l}x=1\\ x=3\end{array}\right.$

Ta có $f\left(x\right)=0\iff -x^3+6x^2-9x=0\iff \left[\begin{array}{l}x=0\\ x=3\end{array}\right.$

và $f\left(x\right)=-4\iff -x^3+6x^2-9x=-4\iff \left[\begin{array}{l}x=1\\ x=4\end{array}\right.$

BBT của hàm số f(x)

Đồ thị (C) cắt trục hoành tại 3 điểm phân biệt có hoành độ thoả mãn $x_1<x_2<x_3$

<=> Phương trình (1) có 3 nghiệm $x_1<x_2<x_3$

<=> Đường thẳng y = m cắt đồ thị hàm số  tại 3 điểm có hoành độ $x_1<x_2<x_3$

Dựa vào BBT ta suy ra $0<x_1<1<x_2<3<x_3<4$