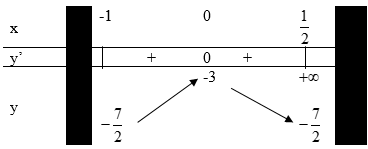
Cho hàm số y = (x^2 - 3x + 3) / (x - 1). Gọi M, m làn lượt là giá trị lớn nhất và giá trị nhỏ nhất
Cho hàm số \(y = \frac{{{x^2} - 3x + 3}}{{x - 1}}\). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \(\left[ { - 1;\frac{1}{2}} \right]\). Tính tích M.m.