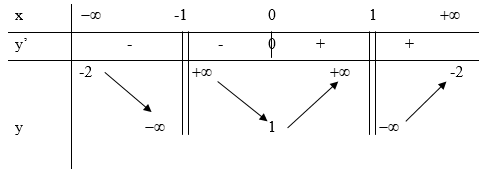
Cho hàm số $y = f\left( x \right)$ xác định trên $\mathbb{R}\backslash \left\{ { \pm 1} \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên hình bên. Tìm tập hợp tất cả các giá trị thực của tham số m sao cho phương trình $f\left( x \right) = m + 1$ vô nghiệm.

D. $\left( { - 2; + \infty } \right)$

Đáp án A

Phương pháp:

Số nghiệm của phương trình $f\left( x \right) = m + 1$ bằng số giao điểm của đồ thị hàm số $y = f\left( x \right)$ và đường thẳng $y = m + 1$

Cách giải:

Phương trình $f\left( x \right) = m + 1$ vô nghiệm $\Leftrightarrow - 2 \le m + 1 < 1 \Leftrightarrow - 3 \le m < 0$