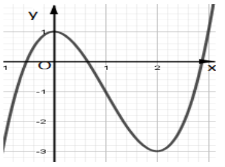
Cho hàm số y = f(x) liên tục trên R và có đồ thị hàm số đường cong trong hình vẽ bên
39
30/04/2024
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị hàm số đường cong trong hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình \(\left| {f\left( x \right)} \right| = m\) có 4 nghiệm phân biệt.
A. \(m \in \left( {0;3} \right)\)
C. Không có giá trị nào của m.
Trả lời
Đáp án D
Phương pháp:
Số nghiệm của phương trình \(\left| {f\left( x \right)} \right| = m\) bằng số giao điểm của đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) và đường thẳng \(y = m\)
Cách giải:
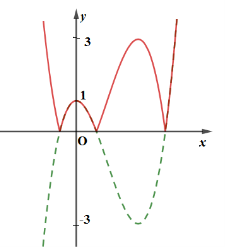
Từ đồ thị hàm số \(y = f\left( x \right)\) ta có đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) như hình bên:
Số nghiệm của phương trình \(\left| {f\left( x \right)} \right| = m\) bằng số giao điểm của đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) và đường thẳng \(y = m\)
\( \Rightarrow \) Để phương trình \(\left| {f\left( x \right)} \right| = m\) có 4 nghiệm phân biệt thì \(1 < m < 3\)