Cho hàm số y = f(x) có bảng biến thiên dưới đây Tìm m để phương trình |f(x)| = m có bốn
Cho hàm số y=f(x) có bảng biến thiên dưới đây
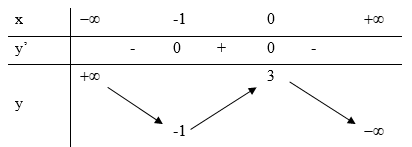
Tìm m để phương trình |f(x)|=m có bốn nghiệm phân biệt
A. 0<m<3
B. −1<m<3
C. 1<m<3
D. m>1
Cho hàm số y=f(x) có bảng biến thiên dưới đây

Tìm m để phương trình |f(x)|=m có bốn nghiệm phân biệt
D. m>1
Đáp án C
Phương pháp:
Lập bảng biến thiên của hàm số y=|f(x)|, từ đó nhận xét số nghiệm của phương trình |f(x)|=m
Cách giải:
Bảng biến thiên của hàm số y=|f(x)|

Số nghiệm của phương trình |f(x)|=m bằng số giao điểm của đồ thị hàm số và đường thẳng y=m, để phương trình |f(x)|=m có bốn nghiệm phân biệt thì 1<m<3