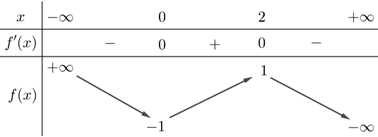
Cho hàm số y = ft( x ) liên tục trên , f( 0 ) = - 1; f( 2 ) = 1; lim x ; - vô cùng f( x ) = + vô cùng; lim x ; + vô cùng f( x ) = - vô cùng. Biết đồ thị y = f'( x ) hình vẽ. Có bao nhiêu
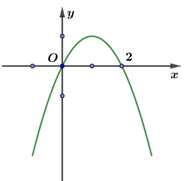
Cho hàm số \[y = f\left( x \right)\] liên tục trên , \[f\left( 0 \right) = - 1;\,f\left( 2 \right) = 1;\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = + \infty ;\,\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - \infty \]. Biết đồ thị \[y = f'\left( x \right)\] hình vẽ. Có bao nhiêu số nguyên \[m\] để phương trình \[f\left( x \right) = m\] có 3 nghiệm phân biệt?
A. \[0\].
B. \[1\].
C. \[2\].
D. \[3\].