Cho hàm số y = f( x ) xác định trên R( 0), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: Hỏi đồ thị hàm số trên có bao nhiêu đường tiệm cận? A. 1. B. 0. C. 2.

64 25/04/2024

Cho hàm số

$y = f\left( x \right)$ xác định trên

$\mathbb{R}\backslash \left\{ 0 \right\}$ , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

Media VietJack

Hỏi đồ thị hàm số trên có bao nhiêu đường tiệm cận?

A. 1.

B. 0.

C. 2.

D. 3.

Trả lời

Lời giải

Chọn A

Dựa vào bảng biến thiên ta có:

$\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = + \infty ;\,\,\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - \infty$ , suy ra đồ thị hàm số không có tiệm cận ngang.

$\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = - 1;\,\,\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = - \infty$ , suy ra đồ thị hàm số có 1 tiệm cận đứng.

Vậy đồ thị hàm số có một đường tiệm cận.

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

Câu hỏi cùng chủ đề

Cho hàm số y = f( x ). Hàm số y = f'( x )có đồ thị như hình bên. Hàm số g( x ) = f( x^2 + 2x) - x^2 - 2x đồng biến trên khoảng nào dưới đây? A. ( - 1 - căn bậc hai của 2 ; - 1).

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

114 10 tháng trước

Cho hàm số y = f( x ) có bảng biến thiên như sau Số nghiệm thuộc [ 0; 3pi /2] của phương trình | f( cos 2x)| = 1 là A. 9 B. 4 C. 7 D. 10

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

97 10 tháng trước

Cho hàm số y = f( x ) xác định, liên tục trên R và có đúng hai điểm cực trị x = - 1,x = 1, có đồ thị như hình vẽ sau: Hỏi hàm số y = f( x^2 - 2x + 1) + 2020 có bao nhiêu điểm cực tiểu?

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

129 10 tháng trước

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy ( ABC), BC = a, góc hợp bởi (SBC) và ( ABC) là 60^0. Mặt phẳng ( P )qua A vuông góc với SC cắt SB,SC lần l

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

95 10 tháng trước

Số điểm cực trị của hàm số f( x ) có đạo hàm f'( x ) = ( x + 1)( x - 2)^2, x thuộc R là A. 0 B. 3 C. 1 D. 2

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

91 10 tháng trước

Đường cong ở hình vẽ dưới đây là đồ thị của hàm số y = ax + b/cx + d với (a,b,c,d) là các số thực. Mệnh đề nào dưới đây đúng ? A. y' < 0, x khác - 1. B. y' > 0, x thuộc R C. y' > 0, x

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

90 10 tháng trước

Cho hàm số y = căn bậc hai của x^2 - 2x - 3. Khẳng định nào sau đây là đúng? A. maxy = 1 B. maxy = 2 C. maxy = 0 D. Hàm số không có giá trị lớn nhất.

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

107 10 tháng trước

Cho hàm số bậc ba y = f( x ) có đồ thị như hình vẽ: Khi đó phương trình 2f( x) - 1 = 0 có bao nhiêu nghiệm thực phân biệt. A. 3. B. 0 C. 1. D. 2.

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

119 10 tháng trước

Tìm tất cả các giá trị thực của tham số m để hàm số y = - 1/3x^3 - mx^2 + ( 2m - 3)x + 2018 nghịch biến trên R A. - 3 nhỏ hơn bằng m nhỏ hơn bằng 1 B. - 3 < m < 1 C. m lớn hơn b

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

132 10 tháng trước

Biết đồ thị hàm số y = f( x ) có một tiệm cận ngang là y = 3. Khi đó đồ thị hàm số y = 2f( x ) - 4 có một tiệm cận ngang là A. y = 3 B. y = 2 C. y = 1 D. y = - 4

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

110 10 tháng trước

Xem tất cả

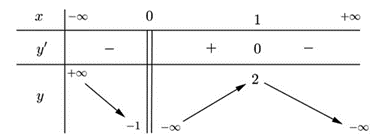
Cho hàm số y = f( x ) xác định trên R( 0), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: Hỏi đồ thị hàm số trên có bao nhiêu đường tiệm cận? A. 1. B. 0. C. 2.

Trả lời

Câu hỏi cùng chủ đề

Cho hàm số y = f( x ). Hàm số y = f'( x )có đồ thị như hình bên. Hàm số g( x ) = f( x^2 + 2x) - x^2 - 2x đồng biến trên khoảng nào dưới đây? A. ( - 1 - căn bậc hai của 2 ; - 1).

Cho hàm số y = f( x ) có bảng biến thiên như sau Số nghiệm thuộc [ 0; 3pi /2] của phương trình | f( cos 2x)| = 1 là A. 9 B. 4 C. 7 D. 10

Cho hàm số y = f( x ) xác định, liên tục trên R và có đúng hai điểm cực trị x = - 1,x = 1, có đồ thị như hình vẽ sau: Hỏi hàm số y = f( x^2 - 2x + 1) + 2020 có bao nhiêu điểm cực tiểu?

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy ( ABC), BC = a, góc hợp bởi (SBC) và ( ABC) là 60^0. Mặt phẳng ( P )qua A vuông góc với SC cắt SB,SC lần l

Số điểm cực trị của hàm số f( x ) có đạo hàm f'( x ) = ( x + 1)( x - 2)^2, x thuộc R là A. 0 B. 3 C. 1 D. 2

Đường cong ở hình vẽ dưới đây là đồ thị của hàm số y = ax + b/cx + d với (a,b,c,d) là các số thực. Mệnh đề nào dưới đây đúng ? A. y' < 0, x khác - 1. B. y' > 0, x thuộc R C. y' > 0, x

Cho hàm số y = căn bậc hai của x^2 - 2x - 3. Khẳng định nào sau đây là đúng? A. maxy = 1 B. maxy = 2 C. maxy = 0 D. Hàm số không có giá trị lớn nhất.

Cho hàm số bậc ba y = f( x ) có đồ thị như hình vẽ: Khi đó phương trình 2f( x) - 1 = 0 có bao nhiêu nghiệm thực phân biệt. A. 3. B. 0 C. 1. D. 2.

Tìm tất cả các giá trị thực của tham số m để hàm số y = - 1/3x^3 - mx^2 + ( 2m - 3)x + 2018 nghịch biến trên R A. - 3 nhỏ hơn bằng m nhỏ hơn bằng 1 B. - 3 < m < 1 C. m lớn hơn b

Biết đồ thị hàm số y = f( x ) có một tiệm cận ngang là y = 3. Khi đó đồ thị hàm số y = 2f( x ) - 4 có một tiệm cận ngang là A. y = 3 B. y = 2 C. y = 1 D. y = - 4

Danh mục