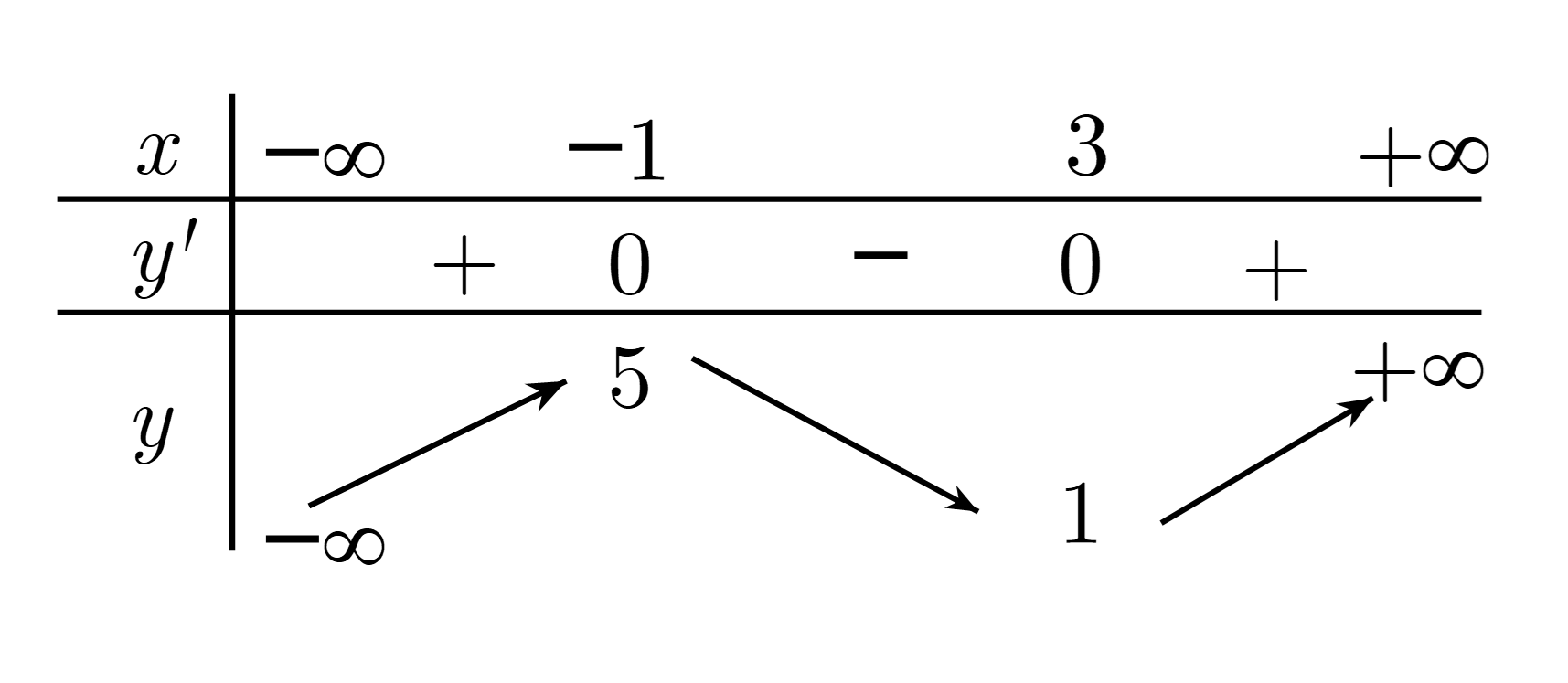Cho hàm số y = f( x ) xác định, liên tục trên R và có bảng biến thiên như sau: Đồ thị hàm số y = | f( x )| có bao nhiêu điểm cực trị? A. 2 B. 3 C. 4 D. 5
55
28/04/2024
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
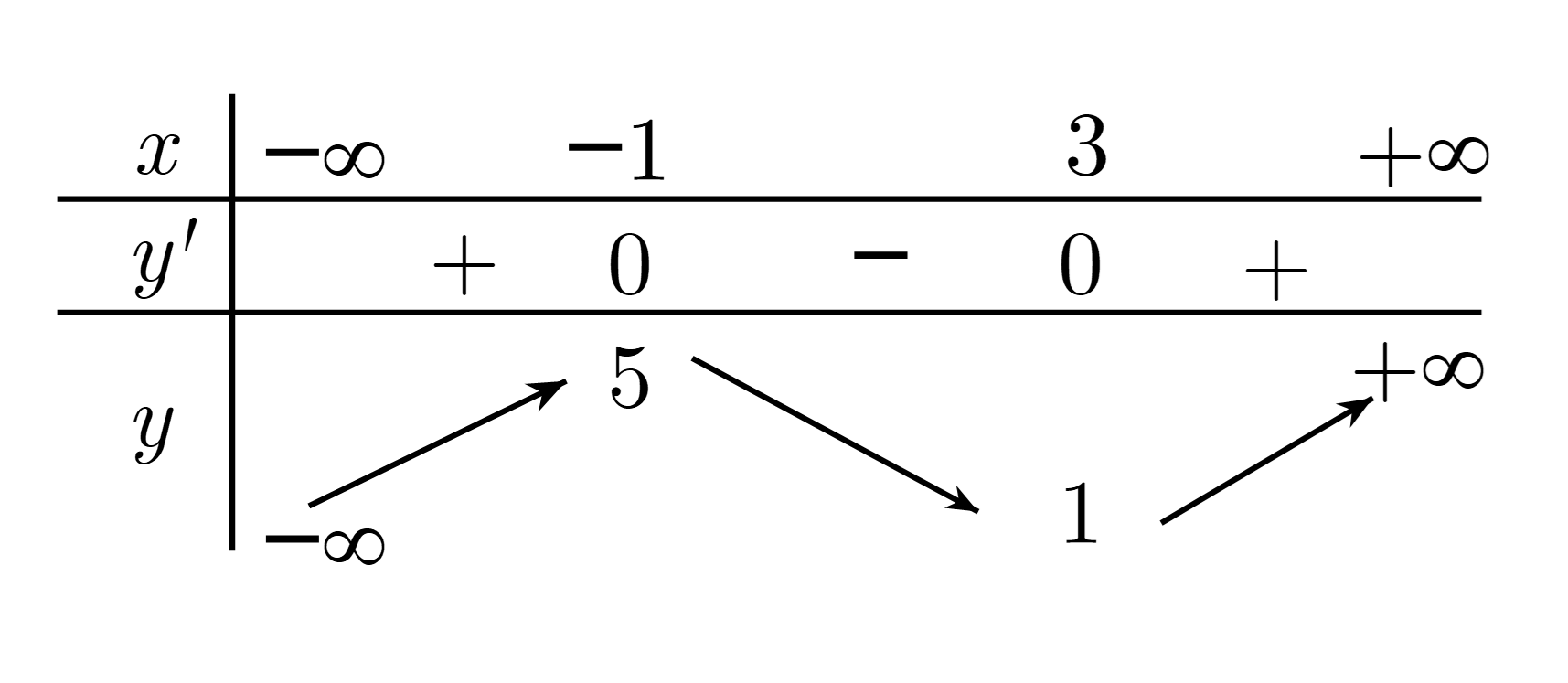
Đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) có bao nhiêu điểm cực trị?
A. \(2\).
B. \(3\).
C. \(4\).
D. \(5\).
Trả lời
Lời giải
Chọn B
Số điểm cực trị của đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) bằng số điểm cực trị của đồ thị hàm số \(y = f\left( x \right)\) cộng với số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) với trục hoành (không tính điểm cực trị).
Vì đồ thị hàm số \(y = f\left( x \right)\) có \(2\) điểm cực trị và cắt trục \(Ox\) tại \(1\) điểm nên đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) có \(2 + 1 = 3\) điểm cực trị.