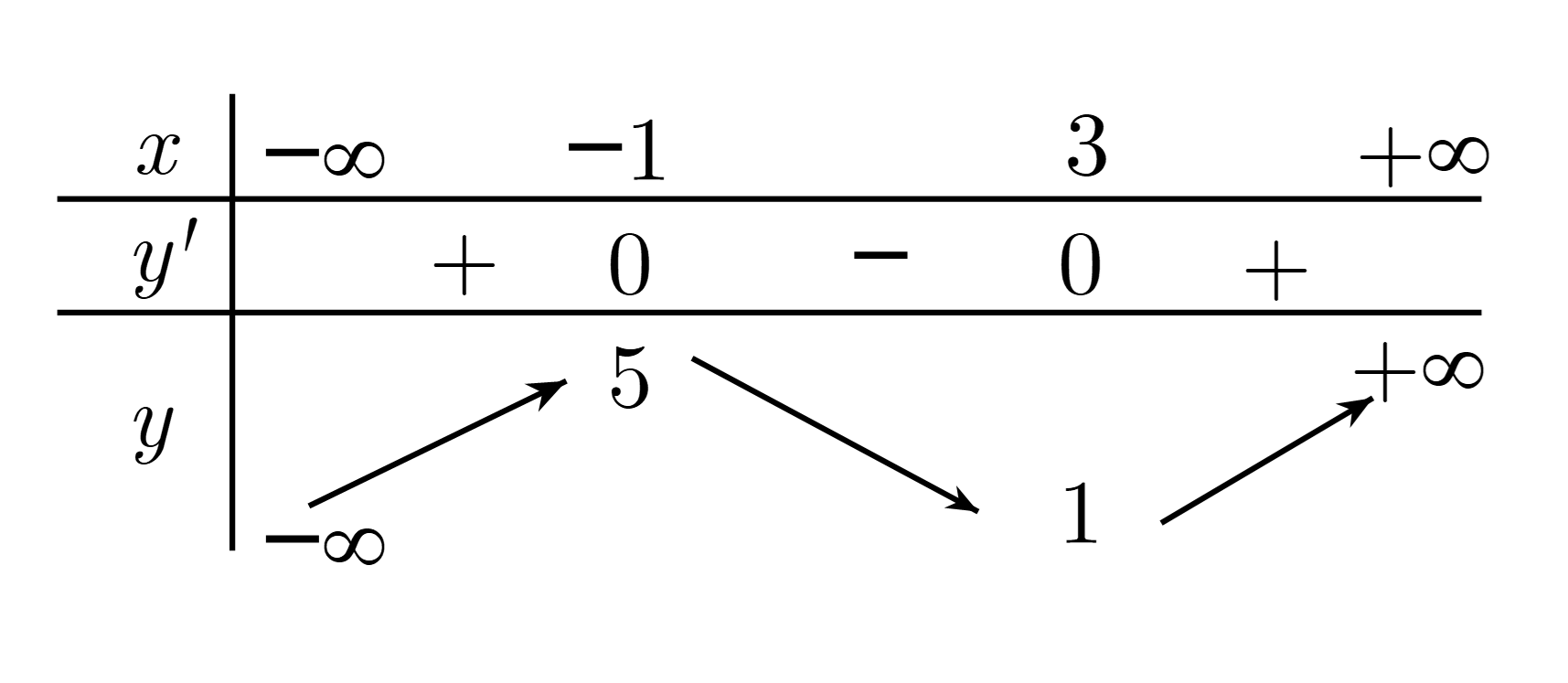Cho hàm số y = f( x ) xác định, liên tục trên R và có bảng biến thiên như sau: Đồ thị hàm số y = | f( x )| có bao nhiêu điểm cực trị? A. 2 B. 3 C. 4 D. 5
79
27/04/2024
Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên như sau:
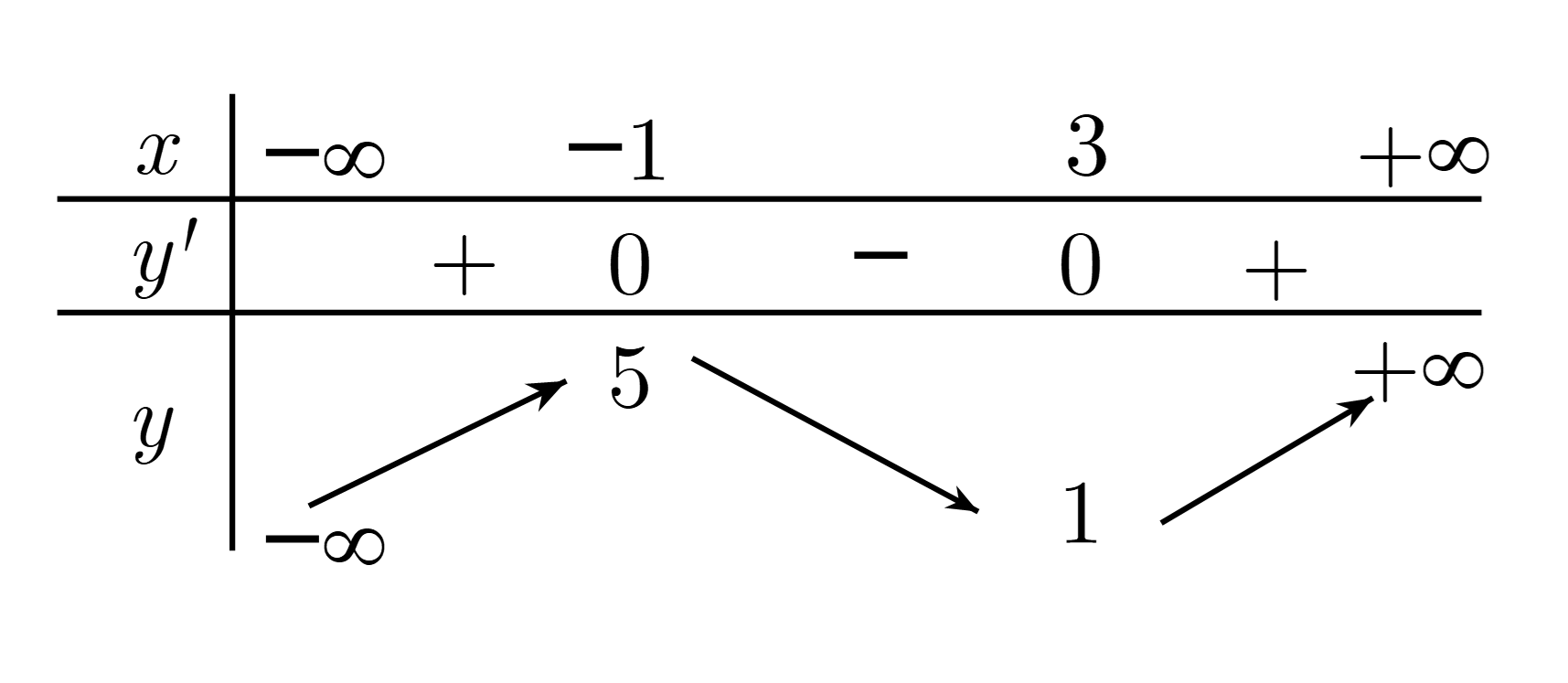
Đồ thị hàm số y=|f(x)| có bao nhiêu điểm cực trị?
A. 2.
B. 3.
C. 4.
D. 5.
Trả lời
Lời giải
Chọn B
Số điểm cực trị của đồ thị hàm số y=|f(x)| bằng số điểm cực trị của đồ thị hàm số y=f(x) cộng với số giao điểm của đồ thị hàm số y=f(x) với trục hoành (không tính điểm cực trị).
Vì đồ thị hàm số y=f(x) có 2 điểm cực trị và cắt trục Ox tại 1 điểm nên đồ thị hàm số y=|f(x)| có 2+1=3 điểm cực trị.
Cách 2:
\left| {f\left( x \right)} \right| = \sqrt {{f^2}\left( x \right)\;} \Rightarrow {\left( {\left| {f\left( x \right)} \right|} \right)^'} = \frac{{f\left( x \right).f'\left( x \right)}}{{\left| {f\left( x \right)} \right|}} \Rightarrow \;dấu của {\left( {\left| {f\left( x \right)} \right|} \right)^'} là dấu của f(x).f′(x)
f′(x)=0⇔x=−1;x=3
Từ bảng biến thiên suy ra f(x)=0⇔x=x0<−1
Lập bảng xét dấu
|
X
|
−∞ x0 -1 3 +∞
|
|
f’(x)
|
+ + 0 - 0 +
|
|
f(x)
|
- 0 + + +
|
|
f'(x).f(x)
|
- 0 + 0 - 0 +
|
Đáp số: 3 cực trị