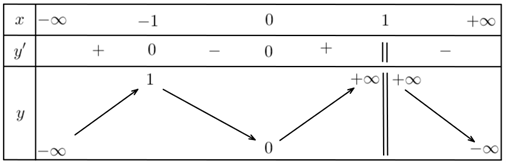
Cho hàm số y = f( x ) xác định, liên tục trên R{ 1 } và có bảng biến thiên ở hình vẽ. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 3 B. 1 C. 2 D. 0
33
04/05/2024
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\backslash \left\{ 1 \right\}\) và có bảng biến thiên ở hình vẽ.
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A. \(3\).
B. \(1\).
C. \(2\).
D. \(0\).
Trả lời
Lời giải
Chọn B
Từ bảng biến thiên ta thấy:
\(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - \infty \) suy ra đồ thị hàm số không có tiệm cận ngang.
\(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = + \infty \); \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = + \infty \) suy ra đồ thị hàm số có \(1\) tiệm cận đứng là \(x = 1\).
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là \(1\).
