Cho hàm số y = f( x ) = | x^4 - 4x^3 + 4x^2 + a|. Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn [ 0;2]. Số giá trị nguyên a thuộc đoạn [ - 3;3] sao cho M
57
28/04/2024
Cho hàm số \(y = f\left( x \right) = \left| {{x^4} - 4{x^3} + 4{x^2} + a} \right|\). Gọi \(M,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn \(\left[ {0;2} \right]\). Số giá trị nguyên \(a\) thuộc đoạn \(\left[ { - 3;3} \right]\) sao cho \(M \le 2m\) là
A. \(3\).
B. \(5\).
C. \(6\).
D. \(7\).
Trả lời
Lời giải
Chọn B
Xét \(g\left( x \right) = {x^4} - 4{x^3} + 4{x^2} + a\) với \(x \in \left[ {0;2} \right]\).
\(g'\left( x \right) = 4{x^3} - 12{x^2} + 8x = 4x\left( {{x^2} - 3x + 2} \right)\); \(g'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 1}\\{x = 2}\end{array}} \right.\).
\(g\left( 0 \right) = a\); \(g\left( 1 \right) = 1 + a\); \(g\left( 2 \right) = a\).
Bảng biến thiên \(g\left( x \right)\)
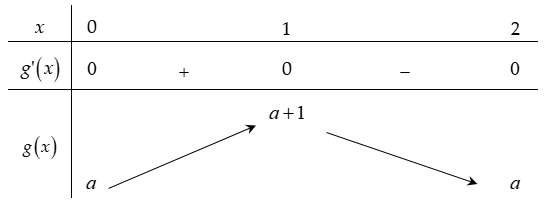
Trường hợp 1: \(a \ge 0\). Khi đó \(M = a + 1\); \(m = a\).
Ta có \(M \le 2m \Leftrightarrow 1 + a \le 2a \Leftrightarrow a \ge 1\). Với \(\left\{ {\begin{array}{*{20}{c}}{a \in \left[ { - 3;3} \right]}\\{a \in Z}\end{array}} \right. \Rightarrow a \in \left\{ {1;2;3} \right\}\).
Trường hợp 2: \(a + 1 \le 0 \Leftrightarrow a \le - 1\). Khi đó \(M = - a\); \(m = - \left( {a + 1} \right)\).
Ta có \(M \le 2m \Leftrightarrow - a \le - 2\left( {a + 1} \right) \Leftrightarrow a \le - 2\). Với \(\left\{ {\begin{array}{*{20}{c}}{a \in \left[ { - 3;3} \right]}\\{a \in Z}\end{array}} \right. \Rightarrow a \in \left\{ { - 3; - 2} \right\}\).
Trường hợp 3: \( - 1 < a < 0\). Với \(\left\{ {\begin{array}{*{20}{c}}{a \in \left[ { - 3;3} \right]}\\{a \in Z}\end{array}} \right. \Rightarrow a \in \emptyset \).
Vậy có 5 giá trị \(a\) cần tìm.
