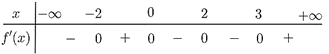Cho hàm số \(y = f\left( x \right)\) thỏa mãn:

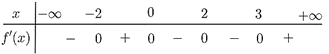
Hàm số \(y = f\left( {3 - x} \right) - x - \sqrt {{x^2} + 2} \) nghịch biến trên khoảng nào sau đây?

Lời giải

Chọn A

Ta có\(y' = - f'\left( {3 - x} \right) - 1 - \frac{x}{{\sqrt {{x^2} + 2} }} \Leftrightarrow y' = - \left( {f'\left( {3 - x} \right) + 1 + \frac{x}{{\sqrt {{x^2} + 2} }}} \right)\).

Ta thấy \(f'\left( {3 - x} \right) > 0 \Leftrightarrow \left[ \begin{array}{l} - 2 < 3 - x < 0\\3 - x > 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}3 < x < 5\\x < 0\end{array} \right.\);

Trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {3;5} \right)\) thì \(1 + \frac{x}{{\sqrt {{x^2} + 2} }}\) đều có giá trị dương.

Suy ra trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {3;5} \right)\) thì:\(f'\left( {3 - x} \right) + 1 + \frac{x}{{\sqrt {{x^2} + 2} }} > 0 \Rightarrow y' < 0\)

Vậy hàm số\(y = f\left( {3 - x} \right) - x - \sqrt {{x^2} + 2} \) nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {3;5} \right)\).