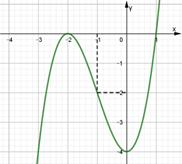
Cho hàm số y = f( x ) liên tục trên R và có đồ thị như hình vẽ. Tập hợp các giá trị thực của tham số m để phương trình f( căn bậc hai của 4x - x^2 - 1) = m có nghiệm là A. [ - 2;0] B
40
01/05/2024
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Tập hợp các giá trị thực của tham số \(m\) để phương trình \(f\left( {\sqrt {4x - {x^2}} - 1} \right) = m\) có nghiệm là
A. \(\left[ { - 2;0} \right]\).
B. \(\left[ { - 4; - 2} \right]\).
C. \(\left[ { - 4;0} \right]\).
D. \(\left[ { - 1;1} \right]\).
Trả lời
Lời giải
Chọn C
Phương trình \(f\left( {\sqrt {4x - {x^2}} - 1} \right) = m\) có điều kiện \(0 \le x \le 4\). Ta có bảng biến thiên
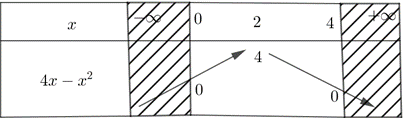
Từ bảng biến thiên suy ra, với \(0 \le x \le 4\) thì \( - 1 \le \sqrt {4x - {x^2}} - 1 \le 1\). Đặt \(t = \sqrt {4x - {x^2}} - 1\), \( - 1 \le t \le 1\). (Có thể biến đổi \(t = \sqrt {4 - {{\left( {x - 2} \right)}^2}} - 1 \Rightarrow - 1 \le t \le 1\)).
Phương trình đã cho trở thành \(f\left( t \right) = m\) (1). Phương trình đã cho có nghiệm \( \Leftrightarrow \) (1) có nghiệm \(t \in \left[ { - 1;1} \right] \Leftrightarrow - 4 \le m \le 0\).