Cho hàm số y = f( x ) liên tục trên R và có đồ thị như hình vẽ sau: Số giá trị nguyên của tham số m để phương trình f^2( sin x) - ( m + 1)f( sin x) + 2m - 2 = 0 có đúng 4 nghiệm thuộc đoạ
37
26/04/2024
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ sau:
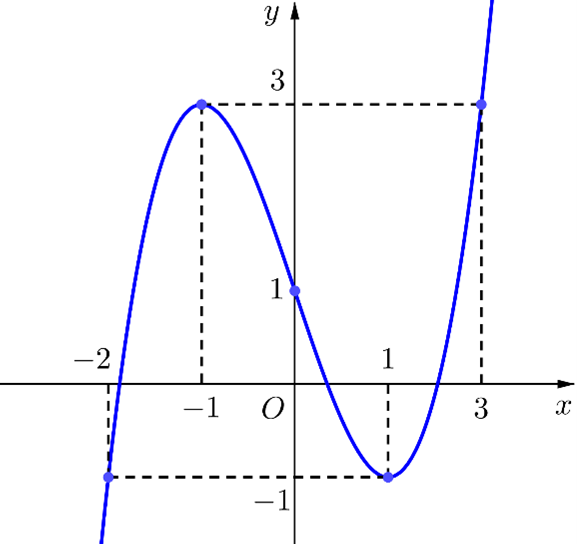
Số giá trị nguyên của tham số \(m\) để phương trình \({f^2}\left( {\sin x} \right) - \left( {m + 1} \right)f\left( {\sin x} \right) + 2m - 2 = 0\) có đúng \(4\) nghiệm thuộc đoạn \(\left[ {0\,;2\pi } \right]\).
A. \(1\).
B. \(2\).
C. \(3\).
D. \(4\).
Trả lời
Lời giải
Ta có \({f^2}\left( {\sin x} \right) - \left( {m + 1} \right)f\left( {\sin x} \right) + 2m - 2 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}f\left( {\sin x} \right) = 2 & \left( 1 \right)\\f\left( {\sin x} \right) = m - 1 & \left( 2 \right)\end{array} \right.\).
Dựa vào đồ thị hàm số \(y = f\left( x \right)\), ta thấy \(f\left( x \right) = 2 \Leftrightarrow \left[ \begin{array}{l}x = a\,\,\left( {a < - 1} \right)\\x = b\,\,\left( { - 1 < b < 0} \right)\\x = c\,\,\left( {1 < c} \right)\end{array} \right.\)
\[\left( 1 \right) \Leftrightarrow \left[ \begin{array}{l}\sin x = a\,\,\left( {a < - 1} \right)\,\,\,\,\,\,\,\,\left( {\rm{L}} \right)\\\sin x = b\,\,\left( { - 1 < b < 0} \right)\\\sin x = c\,\,\left( {1 < c} \right)\,\,\,\,\,\,\,\,\,\,\,\,\left( {\rm{L}} \right)\end{array} \right.\].
Phương trình \(\sin x = b\,\,\left( { - 1 < b < 0} \right)\) có \(2\) nghiệm phân biệt thuộc đoạn \(\left[ {0\,;2\pi } \right]\).
Đặt \(t = \sin x \Rightarrow t' = \cos x\), xét \(t' = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{2}\\x = \frac{{3\pi }}{2}\end{array} \right.\).
Bảng biến thiên
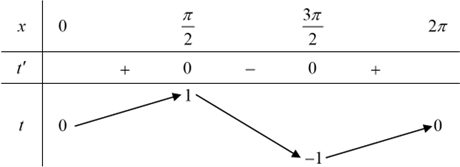
+) Với \({t_0} = - 1\) hay \({t_0} = 1\), phương trình \(\sin x = {t_o}\) có \(1\) nghiệm \[{x_0}\].
+) Với \({t_0} \in \left( { - 1\,;0} \right)\) hay \({t_0} \in \left( {0\,;1} \right)\), phương trình \(\sin x = {t_o}\) có \(2\) nghiệm \[{x_0}\] phân biệt.
+) Với \({t_0} = 0\), phương trình \(\sin x = {t_o}\) có \(3\) nghiệm \[{x_0}\] phân biệt.
Với cách đặt \(t = \sin x\) thì phương trình \(\left( 2 \right)\) trở thành \(f\left( t \right) = m - 1\) \(\left( 3 \right)\)
Yêu cầu bài toán \( \Leftrightarrow \) phương trình \(\left( 3 \right)\) có duy nhất \(1\) nghiệm \({t_0}\) sao cho \({t_0} \in \left( { - 1\,;0} \right)\) hay \({t_0} \in \left( {0\,;1} \right)\) đồng thời nghiệm của phương trình \(\left( 1 \right)\) và \(\left( 2 \right)\) phải khác nhau.
\[ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l} - 1 < m - 1 < 1\\1 < m - 1 < 3\end{array} \right.\\m - 1 \ne 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}0 < m < 2\\2 < m < 4\end{array} \right.\\m \ne 3\end{array} \right.\], mà \(m \in \mathbb{Z}\) suy ra \(m = 1\).
Vậy có \(1\) giá trị nguyên của tham số \(m\) thoả mãn yêu cầu bài toán.


