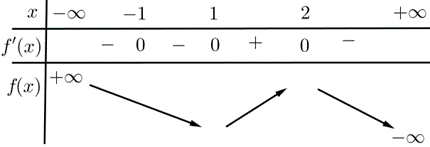
Cho hàm số y = f( x ) liên tục trên R và có đạo hàm f'( x ) = ( x + 1)^2( x - 1)^3( 2 - x). Hàm số y = f( x ) đồng biến trên khoảng nào dưới đây? A. ( - vô cùng; - 1 ). B. ( - 1;1).
Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}\] và có đạo hàm \[f'\left( x \right) = {\left( {x + 1} \right)^2}{\left( {x - 1} \right)^3}\left( {2 - x} \right)\]. Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng nào dưới đây?
A. \(\left( { - \infty \,;\, - 1} \right)\).
B. \(\left( { - 1\,;\,1} \right)\).
C. \(\left( {2\,;\, + \infty } \right)\).
D. \(\left( {1\,;\,2} \right)\).