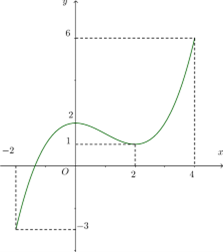
Cho hàm số y = f( x ) liên tục trên đoạn [ - 2;4] và có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình 3f( x ) - 5 = 0 trên đoạn [ - 2;4] là A. 1 B. 0 C. 3 D. 2
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 2;4} \right]\)và có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình \(3f\left( x \right) - 5 = 0\)trên đoạn \(\left[ { - 2;4} \right]\)là
A. \(1\).
B. \(0\).
C. \(3\).
D. \(2\).
