Cho hàm số y = f( x ) là hàm đa thức bậc 3 và có bảng biến thiên như sau Số nghiệm của phương trình f( sin x + căn bậc hai của 3cos x) = 0 trong đoạn [ 0; 5pi /2] là A. 2 B. 4. C
50
05/05/2024
Cho hàm số \(y = f\left( x \right)\) là hàm đa thức bậc 3 và có bảng biến thiên như sau
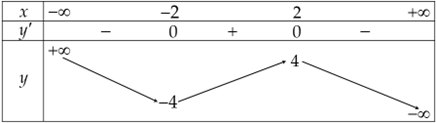
Số nghiệm của phương trình\(f\left( {\sin x + \sqrt 3 \cos x} \right) = 0\)trong đoạn \(\left[ {0;\frac{{5\pi }}{2}} \right]\) là
A. \(2\).
B. 4.
C. 3.
D. 1.
Trả lời
Lời giải
Chọn A
Đặt \(t = \sin x + \sqrt 3 \cos x\). Ta có \(t = 2\cos \left( {x - \frac{\pi }{6}} \right) \Rightarrow - 2 \le t \le 2\). Ta được PT \(f\left( t \right) = 0\).
Dựa vào BBT ta thấy đồ thị hàm số có 2 điểm cực trị là \(\left( { - 2; - 4} \right)\) và \(\left( {2;4} \right)\) nên đồ thị có điểm uốn là gốc tọa độ \(O\). Do đó đồ thị cắt trục hoành tại 3 điểm có hoành độ lần lượt là \(x = a\left\langle { - 2,x = 0,x = b} \right\rangle 2\). Mà \( - 2 \le t \le 2\) nên PT \(f\left( t \right) = 0\) có 1 nghiệm là \(t = 0\).
Với \(t = 0\) ta được \(2\cos \left( {x - \frac{\pi }{6}} \right) = 0 \Leftrightarrow x - \frac{\pi }{6} = \frac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right) \Leftrightarrow x = \frac{{2\pi }}{3} + k\pi \left( {k \in \mathbb{Z}} \right)\).
Theo yêu cầu bài: \(0 \le x \le \frac{{5\pi }}{2} \Leftrightarrow 0 \le \frac{{2\pi }}{3} + k\pi \le \frac{{5\pi }}{2} \Leftrightarrow - \frac{2}{3} \le k \le \frac{{11}}{6}\).
Vì \(k \in \mathbb{Z} \Rightarrow k = 0;k = 1\). Ta được 2 nghiệm \(x = \frac{{2\pi }}{3}\) và \(x = \frac{{5\pi }}{3}\) thỏa yêu cầu bài toán.

