Cho hàm số y = f( x ). Hàm số y = f'( x )có đồ thị như hình vẽ. Hàm số y = f( x^2 - 2) - ( x^3/3 + x^2 - 3x + 4) nghịch biến trong khoảng nào dưới đây? A. ( - vô cùng ; - căn bậc ha
49
01/05/2024
Cho hàm số y=f(x). Hàm số y=f′(x)có đồ thị như hình vẽ.
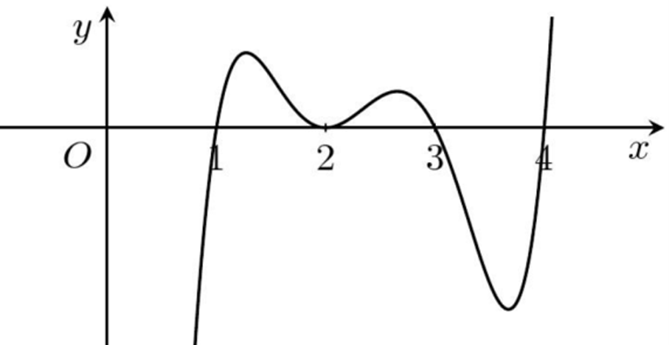
Hàm số y=f(x2−2)−(x33+x2−3x+4)nghịch biến trong khoảng nào dưới đây?
A. (−∞;−√3).
B. (−3;0).
C. (1;√3).
D. (−√3;+∞).
Trả lời
Lời giải
Chọn C
Chọn f′(x)=(x−1)(x−2)2(x−3)(x−4)
Đặt y=g(x)=f(x2−2)−(x33+x2−3x+4).
Khi đó g′(x)=2x.f′(x2−2)−(x2+2x−3).
=2x.(x2−2−1)(x2−2−2)2(x2−2−3)(x2−2−4)−(x2+2x−3)=2x.(x2−3)(x2−4)2(x2−5)(x2−6)−(x2+2x−3)
g′(−2)=3>0
g′(3)=10788>0
Cách 2: (TV phản biện)
Ta có y′=g′(x)=2x.f′(x2−2)−(x2+2x−3)
Từ đồ thị ta có f′(x2−2)<0⇔[x2−2<13<x2−2<4⇔[x∈(−√3;√3)x∈(−√6;−√5)∪(√5;√6).
Suy ra 2xf′(x2−2)<0⇔x∈(−∞;−√6)∪(−√5;−√3)∪(0;√3)∪(√5;√6)
Nên ta lập được bảng xét dấu của g′(x)như sau

Từ bảng xét dấu ta thấy hàm số đã cho nghịch biến trên các khoảng (−∞;−3), (1;√3)và (√5;√6).
Vậy đáp án đúng là đáp án


