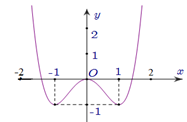
Cho hàm số y = f( x )có đồ thị như hình vẽ bên dưới. Số nghiệm thực của bất phương trình 1 + f( x^3 - 3x^2 + 1) lớn hơn bằng căn bậc hai của 2f^2( x^3 - 3x^2 + 1) + 2 là A. 5 B. 4 C. 3

Lời giải
Chọn A
Đặt \(a = f\left( {{x^3} - 3{x^2} + 1} \right)\) ta được bất phương trình
\(1 + a \ge \sqrt {2{a^2} + 2} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{1 + a \ge 0}\\{1 + 2a + {a^2} \ge 2{a^2} + 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a \ge - 1}\\{{{\left( {a - 1} \right)}^2} \le 0}\end{array}} \right. \Leftrightarrow a = 1\).
Với \(a = 1\) ta được \(f\left( {{x^3} - 3{x^2} + 1} \right) = 1\). Đặt \(t = {x^3} - 3{x^2} + 1\) ta được PT \(f\left( t \right) = 1\left( * \right)\).
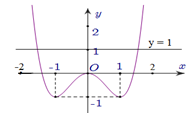
Vẽ đường thẳng \(y = 1\) lên đồ thị đã cho ta được PT \(\left( * \right)\)có 1 nghiệm \(t = {t_1} \in \left( { - 2; - 1} \right)\) và 1 nghiệm \(t = {t_2} \in \left( {1;2} \right)\).
Ta có BBT của hàm số \(y = {x^3} - 3{x^2} + 1\) như sau
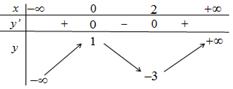
Với \(t = {t_1}\) ta được PT \({x^3} - 3{x^2} + 1 = {t_1}\). Dựa vào BBT ta thấy PT này có 3 nghiệm phân biệt.
Với \(t = {t_2}\) ta được PT \({x^3} - 3{x^2} + 1 = {t_2}\). Dựa vào BBT ta thấy PT này có 1 nghiệm.
Vậy BPT đã cho có 4 nghiệm thực.