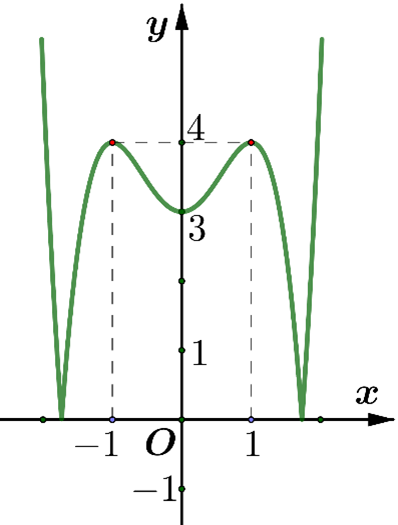
Cho hàm số y = f( x ) có đồ thị là đường cong trong hình dưới đây. Tìm tất cả các gía trị thực của tham số m để phương trình | f (x)| = m có hai nghiệm phân biệt? A. 0 < m < 3; m > 4
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình dưới đây. Tìm tất cả các gía trị thực của tham số \(m\) để phương trình \(\left| {f\left( x \right)} \right| = m\) có hai nghiệm phân biệt?
A. \(\left[ {\begin{array}{*{20}{c}}{0 < m < 3}\\{m > 4}\end{array}} \right.\).
B. \(m > 4\).
C. \(\left[ {\begin{array}{*{20}{c}}{m > - 3}\\{m = - 4}\end{array}} \right.\).
D. \(\left[ {\begin{array}{*{20}{c}}{m > 4}\\{m = 0}\end{array}} \right.\).