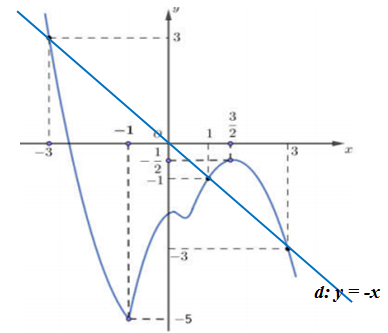
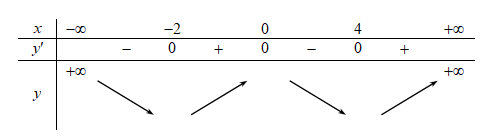
Cho hàm số y = f( x ) có đồ thị f'( x ) như hình vẽ Hàm số y = f( 1 - x) + x^2/2 - x nghịch biến trên khoảng A. ( - 2;0). B. ( 1;3). C.( - 1;3/2). D. ( - 3;1).
70
05/05/2024
Cho hàm số \(y = f\left( x \right)\) có đồ thị \(f'\left( x \right)\) như hình vẽ
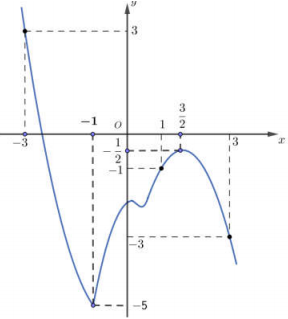
Hàm số \(y = f\left( {1 - x} \right) + \frac{{{x^2}}}{2} - x\) nghịch biến trên khoảng
A. \(\left( { - 2;0} \right)\).
B. \(\left( {1;3} \right)\).
C. \(\left( { - 1;\frac{3}{2}} \right)\).
D. \(\left( { - 3;1} \right)\).
Trả lời
Lời giải
Chọn B
Xét hàm số \(y = f\left( {1 - x} \right) + \frac{{{x^2}}}{2} - x\) có \(y' = - f'\left( {1 - x} \right) + x - 1\).
\(y' = 0 \Leftrightarrow - f'\left( {1 - x} \right) + x - 1 = 0 \Leftrightarrow f'\left( {1 - x} \right) = - \left( {1 - x} \right) \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{1 - x = - 3}\\{1 - x = 1}\\{1 - x = 3}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 4}\\{x = 0}\\{x = - 2}\end{array}} \right.\).
Ta có bảng biến thiên:
Do đó Hàm số \(y = f\left( {1 - x} \right) + \frac{{{x^2}}}{2} - x\) nghịch biến trên khoảng \(\left( {1;3} \right)\).
