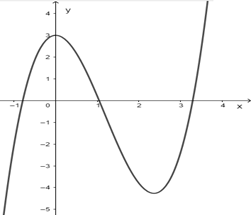
Cho hàm số y = f( x ) có đạo hàm trên R và có đồ thị là đường cong như hình vẽ. Đặt g( x ) = - 2f( fx ) + 3. Tìm số điê
71
27/04/2024
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và có đồ thị là đường cong như hình vẽ. Đặt \(g\left( x \right) = - 2f\left( {f\left( x \right)} \right) + 3\). Tìm số điểm cực trị của hàm số \(g\left( x \right)\).
A. \(2\).
B. \(8\).
C. \(10\).
D. \(6\).
Trả lời
Lời giải
* Ta có: \(g\left( x \right) = - 2f\left( {f\left( x \right)} \right) + 3\); \(g'\left( x \right) = - 2.f'(x).f'\left[ {f(x)} \right]\)
* \(f'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = a\,\,,\,\,\,\,\,\,\,\,\,\,\,\,a \in (2,\,3)\end{array} \right.\).
* \(g'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}f'(x) = 0\\f'\left[ {f(x)} \right] = 0\,\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0,\,\,x = a\\f(x) = 0\\f(x) = a\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0,\,\,x = a\\x = {x_1},\,\,x = {x_4},\,\,x = {x_5}\\x = {x_2},\,\,x = {x_3},\,\,x = {x_6}\end{array} \right.\)
* Gọi \(\alpha = f(a) \in ( - 5,\,\, - 4)\).
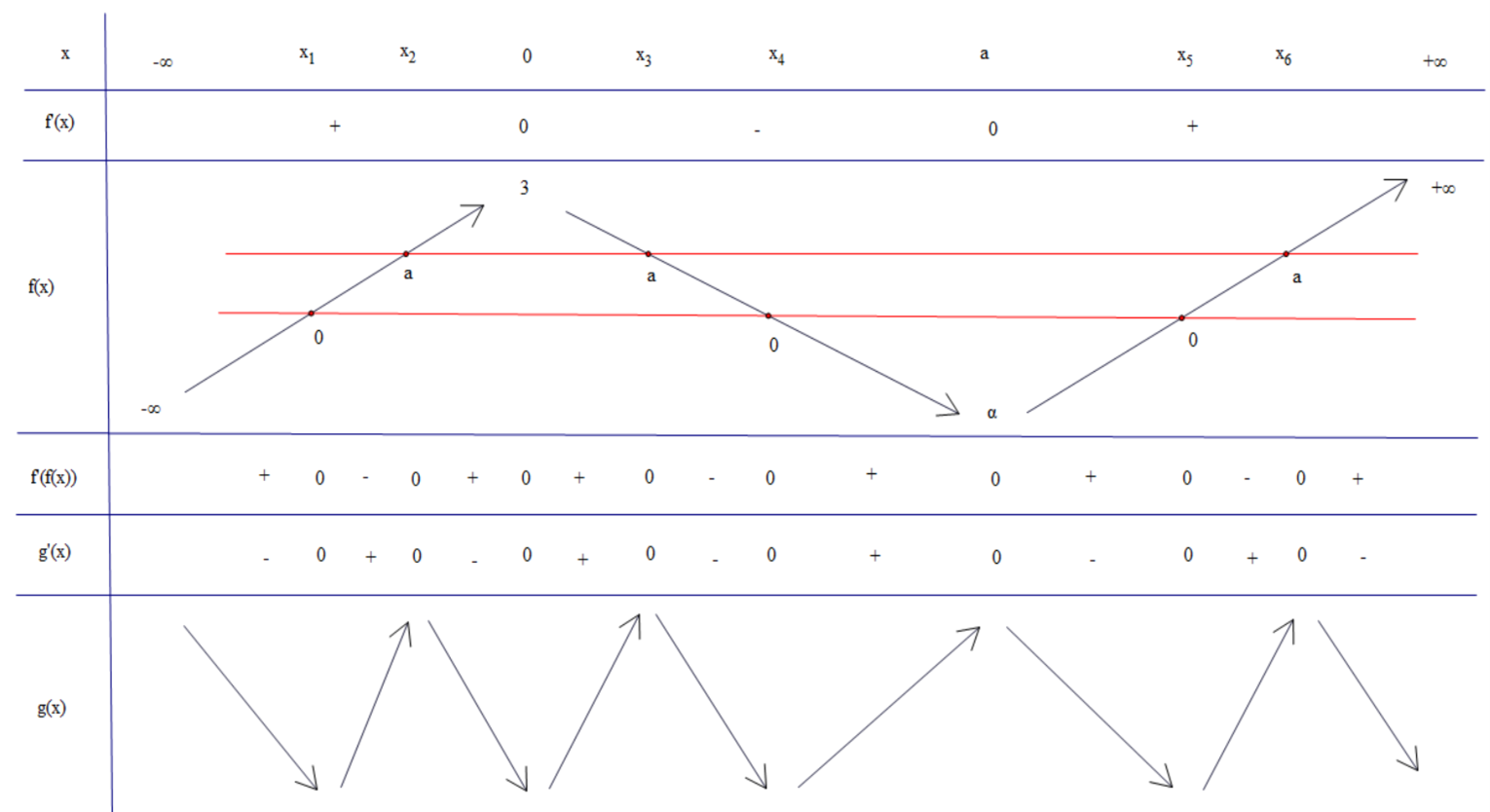
* Ghép bảng biến thiên:
Kết luận: Hàm số \(g\left( x \right)\) có 8 điểm cực trị.


