Cho hàm số y = f( x )có đạo hàm trên R và có bảng biến thiên như hình vẽ Hàm số g( x ) = 3f( 2 - x) + x^3 - 3x đạt cực đại tại điểm A. x = 1 B. x = - 1 C. x = 3 D. x = 2
42
29/04/2024
Cho hàm số \(y = f\left( x \right)\)có đạo hàm trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ
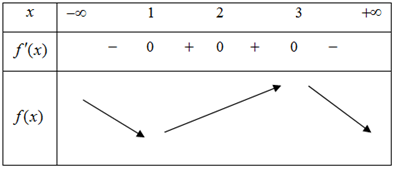
Hàm số \(g\left( x \right) = 3f\left( {2 - x} \right) + {x^3} - 3x\) đạt cực đại tại điểm
A. \(x = 1\).
B. \(x = - 1\).
C. \(x = 3\).
D. \(x = 2\).
Trả lời
Lời giải
Chọn B
Ta có \(g'\left( x \right) = - 3f'\left( {2 - x} \right) + 3{x^2} - 3\).
Từ bảng biến thiên của hàm số \(y = f\left( x \right)\) ta thấy:
\(f'\left( {2 - x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}2 - x = 1\\2 - x = 2\\2 - x = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 0\\x = - 1\end{array} \right.\)
\(f'\left( {2 - x} \right) > 0 \Leftrightarrow \left\{ \begin{array}{l}2 - x > 1\\2 - x < 3\\2 - x \ne 2\end{array} \right. \Leftrightarrow x \in \left( { - 1;1} \right)\backslash \left\{ 0 \right\}\)
\(f'\left( {2 - x} \right) < 0 \Leftrightarrow \left[ \begin{array}{l}2 - x < 1\\2 - x > 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 1\\x < - 1\end{array} \right.\). Ta có bảng biến thiên của hàm số \(g\left( x \right)\):
(Nhờ thầy vẽ lại BBT ạ)
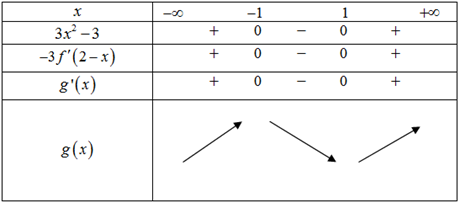
Từ bảng biến thiên ta thấy hàm số \(g\left( x \right)\) đạt cực đại tại \(x = - 1\).


