Cho hàm số y = f( x ) có đạo hàm liên tục trên R và có đồ thị như hình vẽ. Số đường tiệm cận đứng của đồ thị hàm số y = x^2 - 1/f^2 ( x ) - 4f( x ) là A. 2 B. 3 C. 4 D. 1
64
26/04/2024
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.
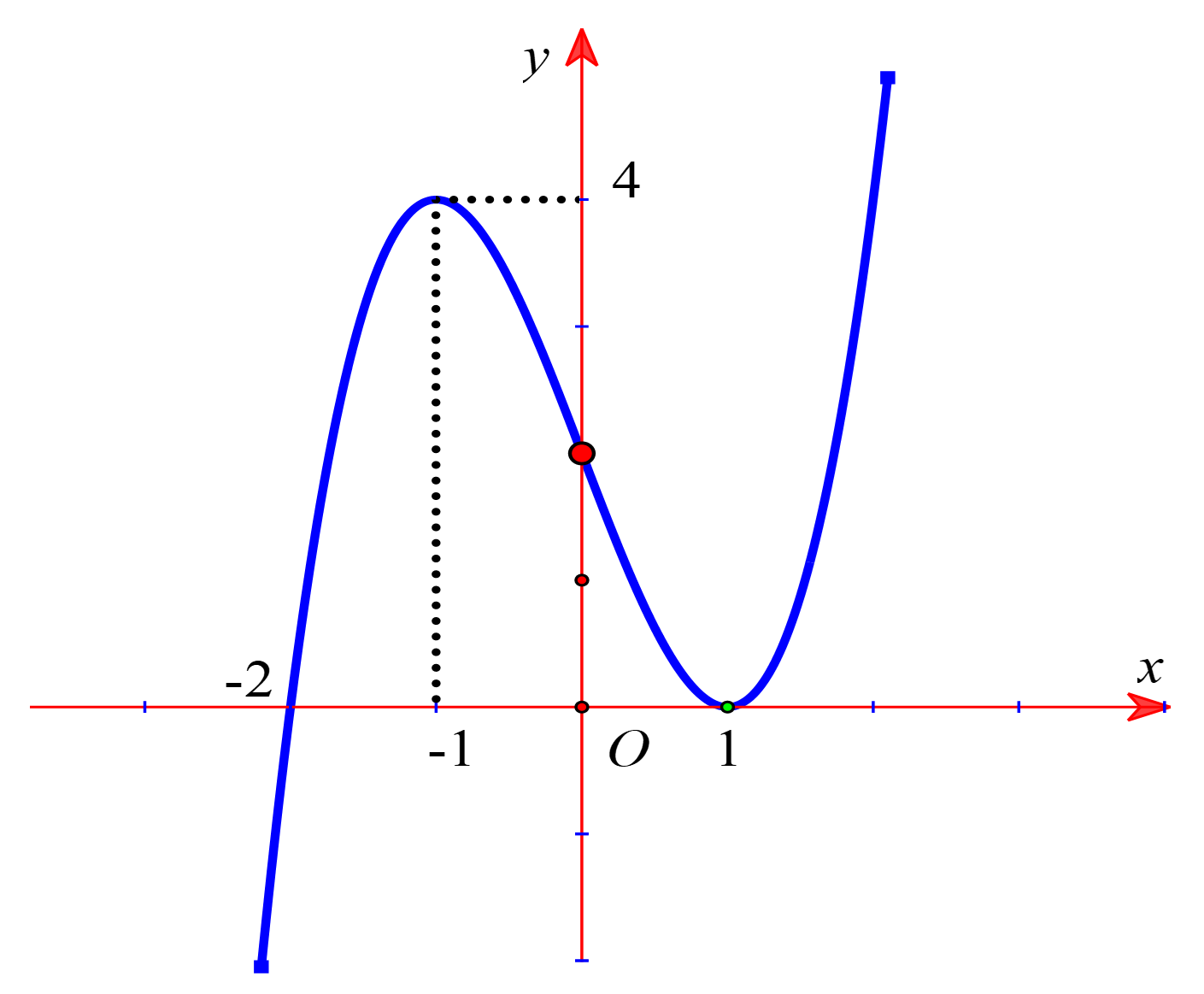
Số đường tiệm cận đứng của đồ thị hàm số \(y = \frac{{{x^2} - 1}}{{{f^2}\left( x \right) - 4f\left( x \right)}}\) là
A. \(2\).
B. \(3\).
C. \(4\).
D. \(1\).
Trả lời
Lời giải
Dựa vào đồ thị, khi đó phương trình \({f^2}(x) - 4f(x) = 0 \Leftrightarrow \left[ \begin{array}{l}f(x) = 0\\f(x) = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 1{\rm{ }}\\x = - 1\\x = 2\end{array} \right.\), trong đó \(x = 1\) và \(x = - 1\) là nghiệm kép bội chẵn. Khi đó
\({f^2}(x) - 4f(x) = \left( {x + 2} \right){\left( {x - 1} \right)^{2k}}\left( {x - 2} \right){\left( {x + 1} \right)^{2l}}.g(x)\), với \(g(x)\) là một đa thức vô nghiệm trên \(\mathbb{R}\) và \(k,l \in {\mathbb{N}^*}\).
Suy ra \(y = \frac{{{x^2} - 1}}{{{f^2}(x) - 4f(x)}} = \frac{{\left( {x + 1} \right)\left( {x - 1} \right)}}{{\left( {x + 2} \right){{\left( {x - 1} \right)}^{2k}}\left( {x - 2} \right){{\left( {x + 1} \right)}^{2l}}.g(x)}}\)
\( = \frac{1}{{\left( {x + 2} \right){{\left( {x - 1} \right)}^{2k - 1}}\left( {x - 2} \right){{\left( {x + 1} \right)}^{2l - 1}}.g(x)}}\)
Vậy đồ thị hàm số \(y = \frac{{{x^2} - 1}}{{{f^2}(x) - 4f(x)}}\)có \(4\) đường tiệm cận đứng đó là \(x = \pm 1,x = \pm 2\).

