Cho hàm số y = f( x ) bảng biến thiên như hình bên dưới Đồ thị hàm số g( x ) = 1/2f( x + 3) + 1 có bao nhiêu tiệm cận đứng? A. 4 B. 3 C. 1 D. 2
36
01/05/2024
Cho hàm số \(y = f\left( x \right)\) bảng biến thiên như hình bên dưới
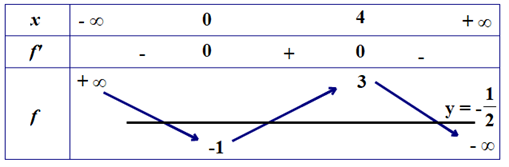
Đồ thị hàm số \(g\left( x \right) = \frac{1}{{2f\left( {x + 3} \right) + 1}}\) có bao nhiêu tiệm cận đứng?
A. \(4\).
B. \(3\).
C. \(1\).
D. \(2\).
Trả lời
Lời giải
Chọn B
Xét phương trình \(2f\left( {x + 3} \right) + 1 \Leftrightarrow f\left( {x + 3} \right) = - \frac{1}{2}\) (*).
Đặt \(t = x + 3\) ta có phương trình trên trở thành \(f\left( t \right) = - \frac{1}{2}\) (**).
Số nghiệm của (**) là số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và đường thẳng \(y = - \frac{1}{2}\).
Từ bảng biến thiên ta có (**) có 3 nghiệm phân biệt, do đó (*) cũng có 3 nghiệm phân biệt.
Vậy đồ thị hàm số \(y = g\left( x \right)\) có 3 tiệm cận đứng.
