Cho hàm số y = f( x ) = ax^3 + bx^2 + cx + d có đồ thị như hình vẽ bên. Khẳng định nào sau đây là đúng? A. a(0,b) 0,c > 0,d > 0. B. a {0,b} 0,c = 0,d > 0 C. a > 0,b {0,c} 0,d > 0. D. a < 0
Cho hàm số y=f(x)=ax3+bx2+cx+d có đồ thị như hình vẽ bên. Khẳng định nào sau đây là đúng?
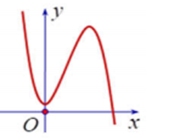
A. a⟨0,b⟩0,c>0,d>0.
B. a⟨0,b⟩0,c=0,d>0.
C. a>0,b⟨0,c⟩0,d>0.
D. a<0,b⟨0,c=0,d⟩0.
