Cho hàm số y = f( x ) = ax^3 + bx^2 + cx + d; ( a khác 0) có đồ thị như hình vẽ. Phương trình f( f( x )) = 0 có bao nhiêu nghiệm thực? A. 5. B. 9. C. 3. D. 7.
102
28/04/2024
Cho hàm số y=f(x)=ax3+bx2+cx+d(a≠0) có đồ thị như hình vẽ.
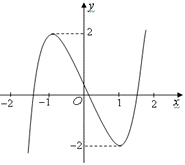
Phương trình f(f(x))=0 có bao nhiêu nghiệm thực?
A. 5.
B. 9.
C. 3.
D. 7.
Trả lời
Lời giải
Chọn B
Từ đồ thị hàm số đã cho trong hình vẽ ta có phương trình f(x)=0 có ba nghiệm phân biệt x1, x2 và x3 thuộc khoảng (−2;2) hay f(x)=0⇔[x=x1x=x2x=x3 với x1, x2và x3 thuộc khoảng (−2;2).
Đặt t=f(x) ta có f(t)=0⇔[t=t1t=t2t=t3 hay [f(x)=t1f(x)=t2f(x)=t3 với t1, t2và t3 thuộc khoảng (−2;2)
Dựa vào đồ thị ta thấy ba đường thẳng phân biệt y=t1, y=t2 và y=t3 mỗi đường thẳng luôn cắt đồ thị hàm số tại ba điểm.
Vậy phương trình f(f(x))=0 có 9 nghiệm.

