Cho hàm số y = ax^3 + bx^2 + cx + d có đồ thị trong hình bên. Hỏi phương trình y = ax^3
61
28/04/2024
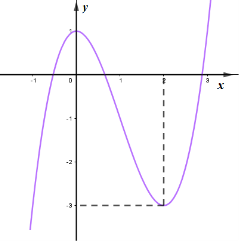
Cho hàm số y=ax3+bx2+cx+d có đồ thị trong hình bên. Hỏi phương trình y=ax3+bx2+cx+2=0 có bao nhiêu nghiệm?
A. Phương trình có đúng một nghiệm.
B. Phương trình có đúng hai nghiệm.
C. Phương trình không có nghiệm.
D. Phương trình có đúng ba nghiệm
Trả lời
Đáp án D
Phương pháp:
Số nghiệm của phương trình ax3+bx2+cx+d+2=0 bằng số giao điểm của đồ thị hàm số y=ax3+bx2+cx+d và đường thẳng y=−2.
Cách giải:
Số nghiệm của phương trình ax3+bx2+cx+d+2=0 bằng số giao điểm của đồ thị hàm số y=ax3+bx2+cx+d và đường thẳng y=−2.
Quan sát đồ thị hàm số, ta thấy: đồ thị hàm số y=ax3+bx2+cx+d cắt đường thẳng y=−2 tại 3 điểm phân biệt ⇒ Phương trình đã cho có đúng ba nghiệm.