Cho hàm số y = ax^3 + bx^2 + cx + d ( a khác 0 ) có bảng biến thiên như sau: Tính S = a + b. A. S = - 1. B. S = - 2. C. S= 1. D. S = 0
45
06/05/2024
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,\left( {a \ne 0} \right)\) có bảng biến thiên như sau:
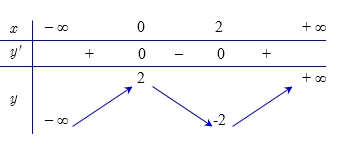
Tính \(S = a + b.\)
A. \(S = - 1.\)
B. \[S = - 2.\]
C. \[S = 1.\]
D. \[S = 0.\]
Trả lời
Lời giải
Chọn B
Ta có: \(y' = 3a{x^2} + 2bx + c\).
Từ bảng biến thiên, ta thấy: hàm số đạt cực trị tại \(x = 0,x = 2\) nên \(y'\left( 0 \right) = y'\left( 2 \right) = 0\).
Đồ thị đi qua các điểm \(\left( {0;2} \right);\left( {2; - 2} \right)\) .
Ta có hệ \(\left\{ \begin{array}{l}y'\left( 0 \right) = 0\\y'\left( 2 \right) = 0\\y\left( 0 \right) = 2\\y\left( 2 \right) = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 0\\12a + 4b + c = 0\\d = 2\\8a + 4b + 2c + d = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 3\\c = 0\\d = 2\end{array} \right.\) . Suy ra \(S = a + b = - 2.\)

