Cho hàm số y = ax + b/cx + 1; ( a, b ,c thuộc R) có bảng biến thiên như sau: Tập các giá trị b là tập nghiệm của bất phương trình nào dưới đây? A. b^2 - 3b + 2 < 0. B. b^3 - 8 < 0.
86
05/05/2024
Cho hàm số \(y = \frac{{ax + b}}{{cx + 1}}\,\,\left( {a\,,b\,,c \in \mathbb{R}} \right)\)có bảng biến thiên như sau:
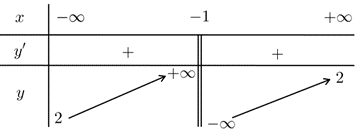
Tập các giá trị \(b\)là tập nghiệm của bất phương trình nào dưới đây?
A. \({b^2} - 3b + 2 < 0.\)
B. \({b^3} - 8 < 0.\)
C. \({b^3} - 8 \le 0.\)
D. \( - {b^2} + 4 > 0.\)
Trả lời
Lời giải
Chọn B
Đồ thị hàm số \(y = \frac{{ax + b}}{{cx + 1}}\)có đường tiệm cận đứng là đường thẳng \(x = - \frac{1}{c}\)và đường tiệm cận ngang là đường thẳng \(y = \frac{a}{c}\).
Nhìn vào bảng biến thiên, ta thấy \( - \frac{1}{c} = - 1 \Rightarrow c = 1\)và \(\frac{a}{c} = 2 \Rightarrow a = 2\)(vì \(c = 1\)).
Ta có \(y' = \frac{{a - bc}}{{{{\left( {cx + 1} \right)}^2}}}\).
Vì hàm số đã cho đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\)và \(\left( { - 1; + \infty } \right)\)nên
\(y' = \frac{{a - bc}}{{{{\left( {bx + c} \right)}^2}}} > 0 \Leftrightarrow a - bc > 0 \Leftrightarrow 2 - b > 0 \Leftrightarrow b < 2 \Leftrightarrow {b^3} < 8 \Leftrightarrow {b^3} - 8 < 0\).
Vậy tập các giá trị \(b\)là tập nghiệm của bất phương trình \({b^3} - 8 < 0.\)

