Chọn A

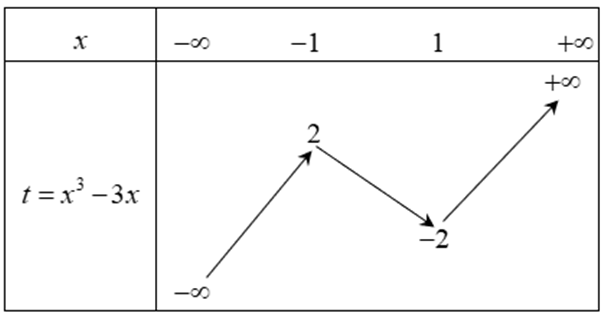
Đặt $t=x^3-3x\begin{array}{cc}& \left(1\right)\end{array}$. Ta có BBT của hàm số $t=x^3-3x$:

Khi đó ta có: $f\left(x^3-3x\right)=m\iff f\left(t\right)=m\iff t^3-3t^2+2=m\begin{array}{cc}& \left(2\right)\end{array}$

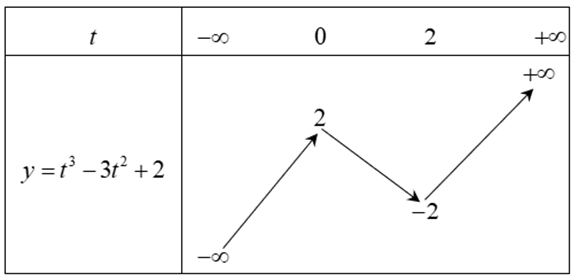
Để phương trình (1) có 7 nghiệm phân biệt thì phương trình (2) có 3 nghiệm t trong đó có 2 nghiệm $t\in \left(-2;2\right)$ và 1 nghiệm t > 2 hoặc t < -2.

Ta có BBT của hàm số $y=t^3-3t^2+2$: