Cho hàm số f(x) có đạo hàm f'(x). Biết đồ thị hàm số y = f'(x) là hình bên. Đặt g(x) = f(x) - x
Cho hàm số f(x) có đạo hàm f′(x). Biết đồ thị hàm số y=f′(x) là hình bên. Đặt g(x)=f(x)−x. Mệnh đề nào sau đây đúng?
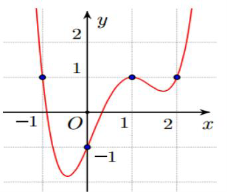
A. g(2)<g(−1)<g(1)
B. g(−1)<g(1)<g(2)
C. g(−1)<g(1)<g(2)
D. g(1)<g(−1)<g(2)
