+) Tìm số điểm cực trị của hàm số \(h\left( x \right)\) bằng cách giải phương trình \(h'\left( x \right) = 0\)

+) Xác định dấu của \(h\left( 0 \right);\,\,h\left( 1 \right);\,\,h\left( { - 1} \right)\) và vẽ đồ thị hàm số \(y = h\left( x \right)\), từ đó vẽ đồ thị hàm số \(y = \left| {h\left( x \right)} \right|\) và kết luận.

Cách giải:

Xét hàm số \(h\left( x \right) = f\left( x \right) - 2017 = a{x^4} + b{x^2} + c - 2017\), với \(a > 0,\,c < 2017,\,\,\,a + b + c < 2017\)

Ta có: \(h'\left( x \right) = 4a{x^3} + 2bx = 2x\left( {2a{x^2} + b} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = - \frac{b}{{2a}}\end{array} \right.\)

Do \(a > 0,\,b < 0 \Rightarrow - \frac{b}{{2a}} > 0\) nên \(h'\left( x \right) = 0\) có 3 nghiệm phân biệt \( \Rightarrow y = h\left( x \right)\) có 3 cực trị

Ta có: \(h\left( 0 \right) = c - 2017 > 0,\,\,\,h\left( { - 1} \right) = h\left( 1 \right) = a + b + c - 2017 < 0\)

\( \Rightarrow h\left( 0 \right).\left( {h - 1} \right) < 0,\,\,\,h\left( 0 \right).h\left( 1 \right) < 0\)

\( \Rightarrow \exists {x_1},\,{x_2}:{x_1} \in \left( { - 1;0} \right),\,\,\,{x_2} \in \left( {0;1} \right)\) mà \(h\left( {{x_1}} \right) = h\left( {{x_2}} \right) = 0\)

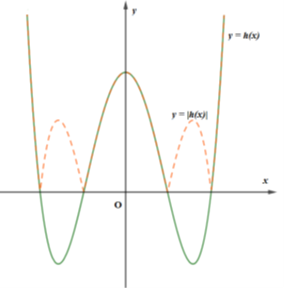
Do đó, đồ thị hàm số \(y = h\left( x \right)\) và \(y = \left| {h\left( x \right)} \right|\) dạng như hình vẽ bên.

Vậy, số cực trị của hàm số \(y = \left| {f\left( x \right) - 2017} \right|\) là 7