Cho hàm số f( x ) xác định trên R và có đồ thị f'( x ) như hình vẽ dưới đây : Đặt g( x ) = f( x ) - x. Hàm số g( x ) đạt cực đại tại điểm thuộc khoảng nào dưới đây? A. ( 3/2;3) B. (

54 27/04/2024

Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}$ và có đồ thị $f'\left( x \right)$ như hình vẽ dưới đây :

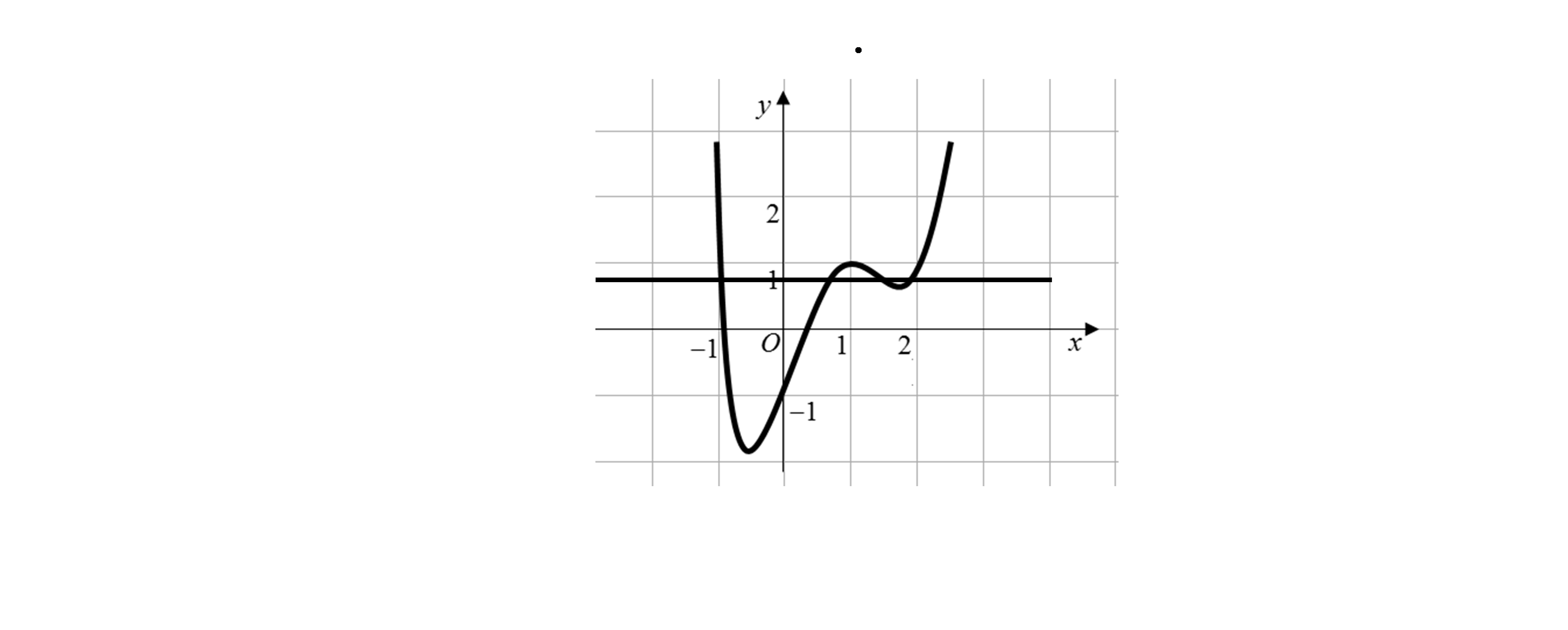
Media VietJack

Đặt

$g\left( x \right) = f\left( x \right) - x$ . Hàm số

$g\left( x \right)$ đạt cực đại tại điểm thuộc khoảng nào dưới đây?

$\left( {\frac{3}{2};3} \right)$ .

$\left( { - 2;0} \right)$ .

$\left( {0;1} \right)$ .

$\left( {\frac{1}{2};2} \right)$ .

Trả lời

Lời giải

Xét hàm số:

$g\left( x \right) = f\left( x \right) - x$ có

$g'\left( x \right) = f'\left( x \right) - 1$

Media VietJack

Từ đồ thị ta thấy phương trình

$g'\left( x \right) = f'\left( x \right) - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = 2\end{array} \right.$

Ta có bảng xét dấu:

$x$	$- \infty$		$- 1$		$1$		$2$		$+ \infty$
$g'\left( x \right)$		$+$	$0$	$-$	$0$	$-$	$0$	$+$

Từ bảng xét dấu ta thấy hàm số

$g\left( x \right)$ đạt cực đại tại

$x = - 1$

Chọn B.

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

Câu hỏi cùng chủ đề

Cho hàm số y = f( x ). Hàm số y = f'( x )có đồ thị như hình bên. Hàm số g( x ) = f( x^2 + 2x) - x^2 - 2x đồng biến trên khoảng nào dưới đây? A. ( - 1 - căn bậc hai của 2 ; - 1).

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

114 11 tháng trước

Cho hàm số y = f( x ) có bảng biến thiên như sau Số nghiệm thuộc [ 0; 3pi /2] của phương trình | f( cos 2x)| = 1 là A. 9 B. 4 C. 7 D. 10

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

98 11 tháng trước

Cho hàm số y = f( x ) xác định, liên tục trên R và có đúng hai điểm cực trị x = - 1,x = 1, có đồ thị như hình vẽ sau: Hỏi hàm số y = f( x^2 - 2x + 1) + 2020 có bao nhiêu điểm cực tiểu?

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

129 11 tháng trước

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy ( ABC), BC = a, góc hợp bởi (SBC) và ( ABC) là 60^0. Mặt phẳng ( P )qua A vuông góc với SC cắt SB,SC lần l

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

95 11 tháng trước

Số điểm cực trị của hàm số f( x ) có đạo hàm f'( x ) = ( x + 1)( x - 2)^2, x thuộc R là A. 0 B. 3 C. 1 D. 2

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

91 11 tháng trước

Đường cong ở hình vẽ dưới đây là đồ thị của hàm số y = ax + b/cx + d với (a,b,c,d) là các số thực. Mệnh đề nào dưới đây đúng ? A. y' < 0, x khác - 1. B. y' > 0, x thuộc R C. y' > 0, x

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

90 11 tháng trước

Cho hàm số y = căn bậc hai của x^2 - 2x - 3. Khẳng định nào sau đây là đúng? A. maxy = 1 B. maxy = 2 C. maxy = 0 D. Hàm số không có giá trị lớn nhất.

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

108 11 tháng trước

Cho hàm số bậc ba y = f( x ) có đồ thị như hình vẽ: Khi đó phương trình 2f( x) - 1 = 0 có bao nhiêu nghiệm thực phân biệt. A. 3. B. 0 C. 1. D. 2.

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

119 11 tháng trước

Tìm tất cả các giá trị thực của tham số m để hàm số y = - 1/3x^3 - mx^2 + ( 2m - 3)x + 2018 nghịch biến trên R A. - 3 nhỏ hơn bằng m nhỏ hơn bằng 1 B. - 3 < m < 1 C. m lớn hơn b

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

132 11 tháng trước

Biết đồ thị hàm số y = f( x ) có một tiệm cận ngang là y = 3. Khi đó đồ thị hàm số y = 2f( x ) - 4 có một tiệm cận ngang là A. y = 3 B. y = 2 C. y = 1 D. y = - 4

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

110 11 tháng trước

Xem tất cả

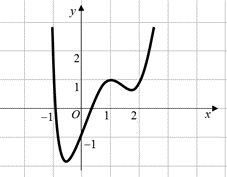
Cho hàm số f( x ) xác định trên R và có đồ thị f'( x ) như hình vẽ dưới đây : Đặt g( x ) = f( x ) - x. Hàm số g( x ) đạt cực đại tại điểm thuộc khoảng nào dưới đây? A. ( 3/2;3) B. (

Trả lời

Câu hỏi cùng chủ đề

Cho hàm số y = f( x ). Hàm số y = f'( x )có đồ thị như hình bên. Hàm số g( x ) = f( x^2 + 2x) - x^2 - 2x đồng biến trên khoảng nào dưới đây? A. ( - 1 - căn bậc hai của 2 ; - 1).

Cho hàm số y = f( x ) có bảng biến thiên như sau Số nghiệm thuộc [ 0; 3pi /2] của phương trình | f( cos 2x)| = 1 là A. 9 B. 4 C. 7 D. 10

Cho hàm số y = f( x ) xác định, liên tục trên R và có đúng hai điểm cực trị x = - 1,x = 1, có đồ thị như hình vẽ sau: Hỏi hàm số y = f( x^2 - 2x + 1) + 2020 có bao nhiêu điểm cực tiểu?

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy ( ABC), BC = a, góc hợp bởi (SBC) và ( ABC) là 60^0. Mặt phẳng ( P )qua A vuông góc với SC cắt SB,SC lần l

Số điểm cực trị của hàm số f( x ) có đạo hàm f'( x ) = ( x + 1)( x - 2)^2, x thuộc R là A. 0 B. 3 C. 1 D. 2

Đường cong ở hình vẽ dưới đây là đồ thị của hàm số y = ax + b/cx + d với (a,b,c,d) là các số thực. Mệnh đề nào dưới đây đúng ? A. y' < 0, x khác - 1. B. y' > 0, x thuộc R C. y' > 0, x

Cho hàm số y = căn bậc hai của x^2 - 2x - 3. Khẳng định nào sau đây là đúng? A. maxy = 1 B. maxy = 2 C. maxy = 0 D. Hàm số không có giá trị lớn nhất.

Cho hàm số bậc ba y = f( x ) có đồ thị như hình vẽ: Khi đó phương trình 2f( x) - 1 = 0 có bao nhiêu nghiệm thực phân biệt. A. 3. B. 0 C. 1. D. 2.

Tìm tất cả các giá trị thực của tham số m để hàm số y = - 1/3x^3 - mx^2 + ( 2m - 3)x + 2018 nghịch biến trên R A. - 3 nhỏ hơn bằng m nhỏ hơn bằng 1 B. - 3 < m < 1 C. m lớn hơn b

Biết đồ thị hàm số y = f( x ) có một tiệm cận ngang là y = 3. Khi đó đồ thị hàm số y = 2f( x ) - 4 có một tiệm cận ngang là A. y = 3 B. y = 2 C. y = 1 D. y = - 4

Danh mục