Lời giải

Chọn B

Tập xác định: \(D = \mathbb{R}\).

Xét \(u\left( x \right) = {x^4} - 4{x^3} + 4{x^2} + m\) liên tục trên \(\left[ {0;2} \right]\).

Ta có \(u'\left( x \right) = 4{x^3} - 12{x^2} + 8x\), \(u'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 1}\\{x = 2}\end{array}} \right.\).

Ta có: \(\left\{ {\begin{array}{*{20}{c}}{u\left( 0 \right) = m}\\{u\left( 1 \right) = m + 1}\\{u\left( 2 \right) = m}\end{array}} \right.\).

Suy ra: \(\left\{ {\begin{array}{*{20}{c}}{\mathop {min}\limits_{\left[ {{\rm{0;2}}} \right]} u\left( x \right) = m}\\{\mathop {{\rm{max}}}\limits_{\left[ {{\rm{0;2}}} \right]} u\left( x \right) = m + 1}\end{array}} \right.\).

\(\mathop {min}\limits_{\left[ {0;2} \right]} f\left( x \right) = \min \left\{ {0;\left| m \right|;\left| {m + 1} \right|} \right\}\) hoặc \(\mathop {min}\limits_{\left[ {0;2} \right]} f\left( x \right) = 0\), với \(m \in \left[ { - 3;3} \right]\) (*).

Trường hợp 1: \(m\left( {m + 1} \right) \le 0 \Leftrightarrow - 1 \le m \le 0\).

      \(\mathop {min}\limits_{\left[ {0;2} \right]} f\left( x \right) = 0\)

Trường hợp 2: \(m > 0\) kết hợp với (*) ta có: \(0 < m \le 3\).

\(\mathop {min}\limits_{\left[ {0;2} \right]} f\left( x \right) = \left| m \right|\).

Trường hợp 3: \(m + 1 < 0 \Leftrightarrow m < - 1\) kết hợp với (*) ta có \( - 3 \le m < - 1\).

\(\mathop {min}\limits_{\left[ {0;2} \right]} f\left( x \right) = \left| {m + 1} \right|\).

Khi đó: \(\mathop {min}\limits_{\left[ {{\rm{0;2}}} \right]} f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\left| m \right|,m \in 0;3}\\{\left| {m + 1} \right|,m \in \left. { - 3; - 1} \right)}\\{0,m \in \left[ { - 1;0} \right]}\end{array}} \right.\).

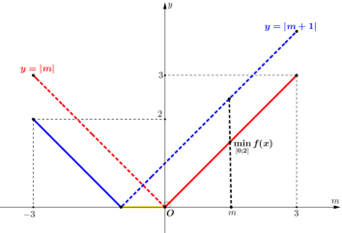
Dựa vào đồ thị ta thấy \(\mathop {min}\limits_{\left[ {{\rm{0;2}}} \right]} f\left( x \right)\) đạt giá trị lớn nhất bằng \(3\) khi \(m = 3\).